5-(-3)の-記号2つ,意味が違うって!
■ 算数・数学を解説・展開しているとき,
①詳しい説明は必要だけど,ここはラフに進める
②(詳しい説明の必要性を自覚せず)ラフに進んでいる
という場面が結構ありそうですね.特に,論理をつなげる小さい,細かい部分・結節点で見受けられます.

■ 数学的には,枝葉部分に相当する細かい個所ですが,少なくするに越したことはありません.児童生徒の目は怖いです.冷静に客観的に見つめられていると覚悟しておきましょう.
■ 約束やルールに根拠を求めること,これは思考の節約や発想の応用のためには必須です.しかし,いつもそればかりだと,算数・数学≓公式の暗記 に繋がりかねません.
■ 暗記は数学教育の中でもっとも遠くへ置くべきです.理解が土台にあって,結果として,「身に付く」形にしたいものです.
8+2×5 の計算
■ 昔風に言えば「乗除は加減に先立つ」となりますが,「かけ算・割り算は足し算・引き算より先に計算する」という算数のルールがあります.
■ 「みなさん! 8+2 だから10 だ!その5倍だから50だ・・・なんてやってないよね.どうするんだっけ.そう,かけ算を先に計算する約束だったよね.すると・・・」
こんな授業展開が想定できます.実際,ありそうですね.
Q1 8+2+2+2+2+2 を計算しましょう.
Q2 2+2+2+2+2 は長いですね.普通,どのように書きますか?
8+2+2+2+2+2 を短く書いてください.
Q3 8+2×5 = 10×5=50 のおかしいところはありませんか?

■ 「8+2×5 を 10×5 としてはいけない」というワケを ”約束だから“,”ルールだから” で済ませてしまうのは,一番ラク.でもそれでは子どもたちが気の毒です.
■ 算数・数学を一度で理解できるヒトは多くありません. 必要に応じてその都度,one point レッスンをする.その積み重ねが”理解”への近道.
■ 授業の進捗状況なども見ながら,Q1~Q3などを参考にして,ワケを子ども自身に考えさせるべきですね.大した時間はかかりません.ちょい足し精神の発揮です.
その際,即”グループ協議突入”は疑問です.まずは,自身で考えなきゃ・考えさせなきゃ.
■ 小さな疑問もスルーさせないという姿勢の有無が,後々,大きな「差」となって表れます.そこが怖い.
3-(-2)⇒ マイナス記号の意味が違う!
■ 3-(-2)についてです.
前の「-」・・・”引く”という演算(operation)
後の「-」・・・”負”の意味で符号(symbol)
をそれぞれ表しています.それらが全く同じ記号「-」で示され(「+」記号も同様),二つの意味が与えられます.しかも,この両者は近場で混在しながら,これまでも・今も・これからも,自由自在に動き回ってフル回転で使用されます.

■ この正負の数の計算について,中1生にどうやって説明するのか,率直に言って戸惑いますね.
■ この稿を起こすため,約半世紀前の中学教科書を読み返してみました.結論から言えば,正負の数については,現在版よりはるかに分かりにくい記述でした.
よくあんなのでナットクしたな~という思いです.
■ 現行教科書を参考に,正負の数の計算について以下のようにまとめてみました(一部).どこまでが定義(ルール)なのか,どれが定理に相当するのか,よく分からなくなりました(⇒ 数学は皆「約束」で成り立っている,などという声もあります).まずは見てください.
なお,演算と符号の記号ですが,多少区別が付くようにしてあります.


■ ここまでの感想です.正負の数の計算指導は,代数学の第一歩だからと論理にこだわり過ぎるのは「ムリ」と思います.だからといって,まったく論理に無頓着で「とにかく答えを求めさせなきゃ.まずパターンを徹底しよう」といった指導態度は勘弁してほしいですね.
■ かつて,演算記号と符号を明確に区別して(例:演算+→ +, 符号+ → +), 解説を図った参考書があったと記憶してますが,結局,「廃れ」ましたね.それまでが計算が得意だった子どもが離れたという話も.中途半端にやると,分かる子も分からなくなってしまったのではと推察します.しかし,演算と符号はベツモノだ,という気持ちはよ~く分かります.興味関心を示す子どもはいますよ,きっと.
「または」 ⇒ 論理用語と日常用語がゴチャ!
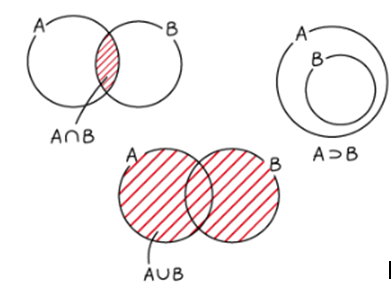
または(or)
・・・「カレー(a) または 牛丼(b)をおごろう」
↓↓
日常語・・・a か bのいずれか一つ
数学論理・・・ベン図で分かるように,重なっている部分(a かつ b)も含まれている
⇒「カレーと牛丼二つともおごってもらってよい」
■ 「数学は世界共通語である」という言葉をご存じかと思います.確かに,たとえば積分記号を用いた式はどこの国でも意味が通ります(はず).
自然数をはじめ,世界共通の記号や式表現を用いるからですね.
■ もちろん,論理の流れ等は各国の母語を用いての説明になりますので,限界があるのは当然.
すると,各国ごと,数学用語と日常用語との齟齬・違いに注意を払う必要があります.
■ 一例を紹介します.「または(or)」です.
■ 教科書の記述で気になるところを見つけました(下:順に中3,高1数学).もちろん,「誤用」ではありませんが,使用されている「または」は日常用語なのか,数学用語なのか,どちらでしょう.あるいは,そんな「細かいところ」は気にしなくてもよいのかな?

■ 中3数学教科書は,日常用語としての使用でしょう.つまり,「3枚とも表」と「2枚表,1枚裏」が同時に成り立つことはあり得ない,という前提で記述されています.
■ 高1数学教科書では,「A=0 かつ B=0」の場合(⇒2次方程式における重解のケース)も含めた「または」となっています.
Q4 最後の行:「求める解は」として” x= -7,4 “ としておりますが,ここで使用された「,」はどんな意味を持っていますか?
⇒ よく,「か」というヒトがいます.つまり,”-7か4” だと.
すると,この「か」は「または」と同じ意味ですか?どこかおかしいですね.
<補足>
■ 次回テーマは「数学と物理の接近」です(予定).算数・数学の担当者が,理科&物理の教科書を読んでいる,関心を持っているという話,ほとんど聞いたことがないですね.そのタイド,間違いです!
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


