「数学 ⇔ 物理」離れすぎ!
■ 数学教育と物理教育に携わるヒトは,もっと接近すべきだと前々から考えてきました.
■双方の接近は,結果として,理数を学ぶヒトに「よさ」が還元されると確信します.

■ 特に,2022年から新学習指導要領がスタートしますが,ベクトルが数学Cに入ったことで,高校生の過半数はベクトルを「言葉すら知らず」に卒業する可能性がかなり高いと予想.
すると,物理の担当者は,ベクトルを「全く新鮮な気持ちで聞く」生徒たちを前に,力学等の解説をしなければなりません.
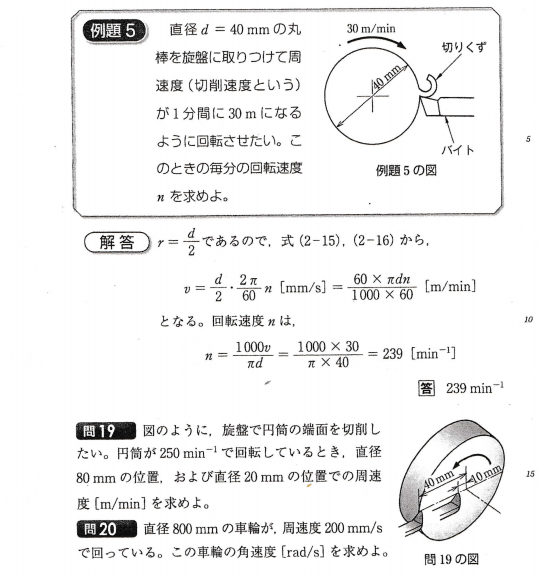
■ 従来以上に,数・物の接近は必要不可欠かと.
運動の公式 ⇔ ほぼ 微分・積分の世界
■ 運動の中で代表的な「落体の運動」について,教科書の主な記述例を紹介します.
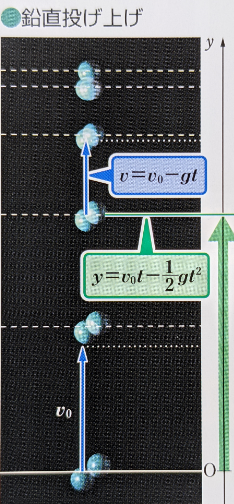
↑投げ上げ点の高さh=0の図(数研出版 フォトサイエンス「物理図録」より)

■ ①②とも解説が”苦しい”ですね.特に,②については,①のグラフを描いて,直線下の台形面積が距離を表すことを確認して,面積計算をしてから結果を出しています.
■ 微積分を学ぶと以下のようになります.

■ ⓪①②の全部が,この中の1つの式だけで代表でき,かつ,即,他の2式を導き出せるということ!これまで,それぞれを独立したものとして理解・暗記してきたことは,実に次元の低いコトだったワケです.例えば,②から①⓪を導いてみます.

■ ①から②を導いてみましょう.微積分を使用しないと解説にエライ苦労します.
(1) 平均の速さ40km/h で2時間走った車は,速さ×時間=40×2 で距離80km 動いたことになるワケですが,縦軸:速さv ,横軸:時間t (vt図という)とすると,v・t は長方形の面積を計算することに相当します.
⇒ 面積が距離を表す!面積は面積だけではないのですね.小学校高学年辺りから意識して当たることがpointになります. ただし,vt図でないと説明付きません.
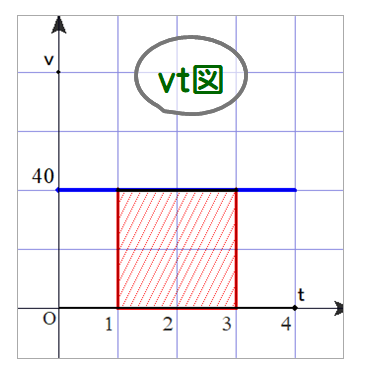
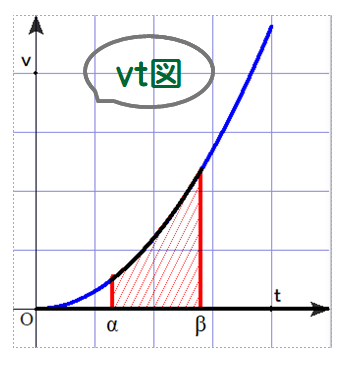
(2) 面積計算は,積分計算とほぼイコールになります.細かいことを言うと,グラフがx軸より下(y<0)の場合は,結果数値に-がつくので,+にする必要がありますが.
以上のことから,①をtで積分すれば②が求められるのです.
y=∫(-gt+v0)dt = -1/2gt2+v0t+h ・・・・②
以上のことから,積分定数の意味が分かります.積分定数は,初速度v0 や 高さh です.つまり,運動を決定付ける重要な要素ですね.
⇒ 数学の授業では「形式的に+C」とするだけの,どちらかと言えば「お飾り」的な扱いをしている向きも? 必反省.
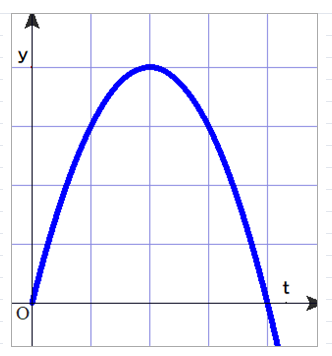
Q ②は,上に凸の放物線を表しますね.小球は鉛直投げ上げです.どうして放物線を描くのですか?
A 図がyt図だからです(上のグラフは h=0 の場合).
yx図なら小球の軌跡を表します.しかし,鉛直投げ上げですので,x=0. ∴y軸上での上下動だけのグラフとなります.
※1 この種の質問は大いに歓迎されるべきです.分かっているようで,実のところ「意識していない ⇒ したがって,答えられない」という例です.
※2 yt図で放物線各点のy軸への正射影が小球の軌跡を示しています.
双方の 乗り入れ授業 ⇒ それは,歓迎されますよ
■ 「物理に微積を大胆に入れる?ムリムリ」という声が聞こえます.
主な理由として
①微積は高2で(半ば過ぎ辺りから),物理の運動等は高1で履修するケースが多い.
②高1の早い段階で微積分を扱うことになるが,生徒の発達段階を考えると現実的ではない.
③特に,数学では,標準履修から大きく違えると,外部模試受験等の場合,試験範囲が全国と合わず,生徒が不利な状況になる.
■ 学習指導要領の中身を再度検討しよう,などという大仰なことを提案しているわけではありません.
各教科それぞれの論理は当然尊重されるべきです.その際,教科間に全く重なる部分がなければよいのですが(例:英語と数学),数学・物理.工業等は互いにかなりの重なり部分を持ちます.
教育サービスを受けるヒト(生徒・学生)は同一人物ですので,その視点から数学や物理の展開に創意工夫をしましょうという提案です.
次は,工業高校の専門教科書の一部です.
■ いかがでしょうか.高校数学担当者からは「こんなレベルの内容を工業高校でやっているの?知らなかった!」という声が大半ではないかと.
三角関数や弧度法,これらはマスターしていなければ,工業高校の専門書を読み解くことはできませんね.
■ 次に,いくつかの話題と提案を
(1) ある工業高校では,数学科との協議をして,高1生について,入学後は三角比からスタートするという方針で進めているそうです.この柔軟性,参考になりますね.
(2) 数・物・工業の教科担当者は,①お互いの教科書に目を通す.②協議する機会を設ける.どうでしょうか.
(3) 物理の「運動」の中で,ある授業で数学科某氏を招待する.某氏は20分ほど微分計算の仕方と意味を押さえる(半年後に詳しく学ぶと伝える).特に,vt図では”面積が距離”を表すことを確実に指導する.

(4) 昨今,少人数対応の一例としてTTが取り入れられていますが,大半が同教科のメンバーです.そこで,数と物のメンバーがTTとなって,それぞれの視点で短時間の教科レッスン指導をくり返す,というのはいかがですか.
例「物理をやっているといつも出てくる弧度なんですが,小学校で習った”円周率”が角を表すことがよく分かんない.円周率だったら円と関わるのが普通.このように,スッキリしないという生徒が大半です.○○先生,弧度の説明とその発想のpointを教えてください」
<補足>
■ 次回テーマは「”減少の鈍化”ってどんなこと?」です(予定).コロナ禍,最近よく耳にする,数値変化を捉える表現ですが,伝わっているでしょうか?ここでは,「微分」まで持ち出してまな板にあげます.
■ 「にほんブログ村」のバナーをclickしていだだければ幸いです(はじめに左, 次に右).


元物理教員としては、尤もなことだと思いましたし、有り難いことと思いました。
教科担当者は、それぞれの責任とプライドを持って授業に当たり、教科の範囲で理想の生徒像を考えていると思います。共通テストへの移行課題にもなっていたと思いますが、「根本を考える力」が今後、ますます問われる時代になると思いますので、教科の見かけの枠に囚われない、広く、深い視点で指導できる、有能な教員がたくさん出てほしいと思います。
コメントをありがとうございました.
教科の枠を超えた,”深い視点で指導できる”という言葉に共感を覚えます.
昨今は「授業形態論」に近い論議が中心ですね.また,その教科自体についてはどうかといえば「問題解き」が大半です.
「根本を考える力」を教科を超えて追究したいものです.
※今回のテーマとは直結しませんが,理学部や文学部等,教員免許取得必修としない大学・学部からの教員希望がかなり減っています(多分間違いない).これはよろしくない傾向と考えています.