このａは定数，変数どっちなんだ！

■ 1次関数 y=ax についてです．yはxの関数ですから，当然x,yは変数になります．では，aは何でしょうか．

⇒ 変数xの係数がaということですので，aは定数（扱い）となります．が，コトはそんなに単純ではないのです．

   

文字だらけの式

Ｑ１ １次関数 g : y=ax-a²   ･･･① について，どんなaについても直線gが通らない領域を求めなさい．

■ この種の問と初対面すると，少なからずのヒトはキョトン「？」とします．文字だらけで何言っているのかわからない，つまり，題意が理解できないのです．

■ ①は，１次関数で，傾き:a, y切片: -a² の直線を表しています．いずれ文字・文字・文字ですね．

“抽象”過ぎる ⇒ “具体”でイメージ

■ a として適当に数を入れてみます．a=1, 1.5, 2（画像は，フリーのグラフソフトgrapesを利用）

 

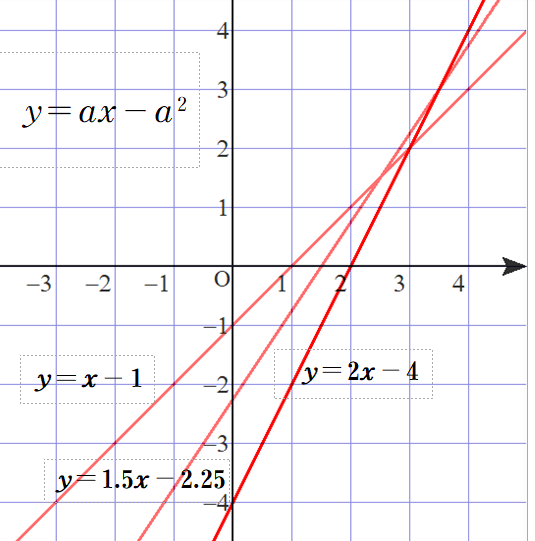
■ 続けて，a=-2, -1.5, -1, 0 とします．

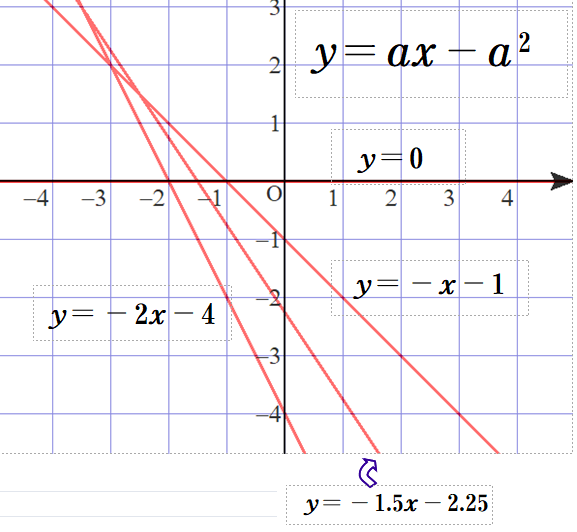
■ 全体の雰囲気が把握できますね．

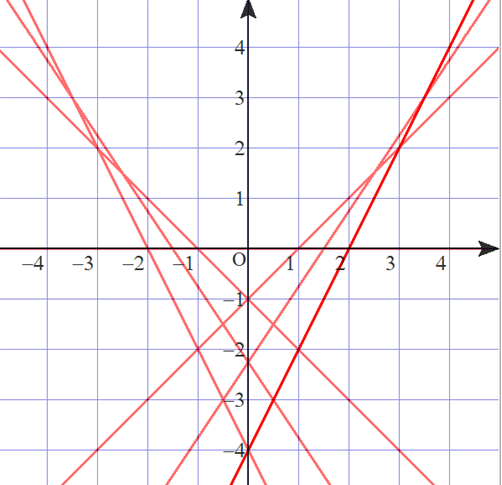
■ 直線の集まり（直線群）が見えます．

ただ，直線gは，かなりの範囲をカバーしていますが，gが”避けている”範囲がありそうです．

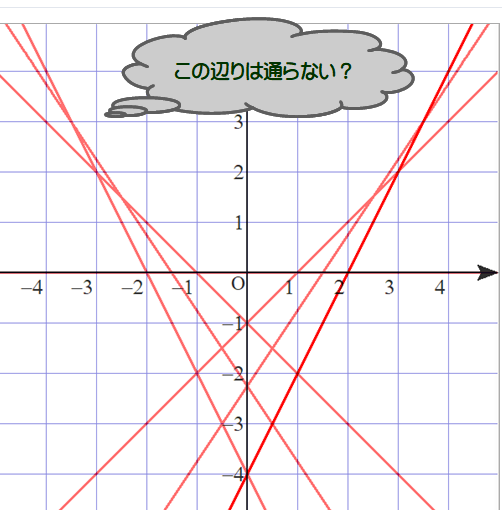
通過できない点の確認

■ 具体に確認してみましょう．たとえば，gは点(1,2)は通らない・通れないようです．

なぜなら，関数式: y=ax-a²  でx=1,y=2 としますと，

　2=a-a²     すなわち，a²-a+2=0    

これは，aについての２次方程式で虚数解をもちます．

グラフとはa,x,yすべてが実数を前提としていますので，この直線は存在できない，よって，gは点(1,2)を通ることはない，となります．

■ これまでの説明を動画で確認しましょう．

　grapesによる説明

Ａ （解答例）

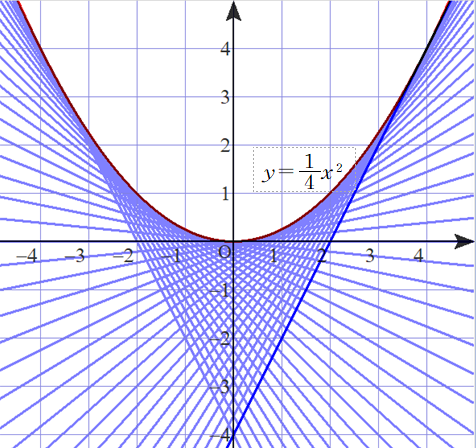
※ 上図で，直線gが通過しない部分は，空白個所，すなわち放物線 y＝1/4x² の上方になります．

＜マトメ＞

■ 例：y=ax-a² について

① a は変数x，yに対しては定数として振る舞う.ここまでは，x,yの１次式．

 y=ax-a² ･･･x,yの１次式

しかし，同値変形することで，aに関する２次方程式の問題へとステージが移動する．　

a²-xa+y=0 ･･･ aの２次式（方程式）

この視点＆ステージの変化を数学的思考として”歓迎”するか，”毛嫌い”するか．

後々，この違いは数学を学ぶ上で大きく響きます．

② aを定数扱いして得られた式において，aは任意の実数であることから，aを変数と見立てて計算を進めることができる．⇒ もちろん，xとaを同時に変数扱いすることは出来ない．

他の例：微分係数：f'(a)は x=a における接線の傾きとして極限値計算により定義される．この後，aは任意の数であることから，改めてxと書き換えたものが，導関数f'(x) である．

＜補足＞

■ 次回テーマは，「三角形面積公式にナットクいかない○さん」（予定）です．鈍角三角形の面積公式にどこか引っ掛かる○さんの「研究発表」です．

■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左，次:右).