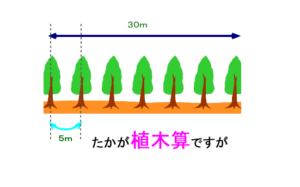
“必要感”を示す数学を
■「数学史を踏まえる」などと大仰な言い方はしませんが,新しいコトを取りあげる際は,その”必要性(or必然性)”を感じさせたいもの.
■ ラーニングをアクティブにするためにも,コトとコトの間にどんな流れや背景があるのかを,体感・追体験することはかなり重要です.学ぶ意欲と直結すると言ってもよいですね.
例をいくつか紹介します.
三平方の定理への誘い
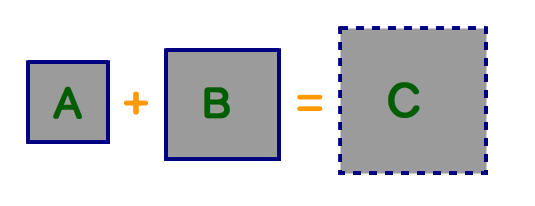
Q1 正方形AとBの面積の和と等しい面積をもつ正方形Cを作図してください.
■ この問は三平方の定理を導入する際,何気なく発問したもの.
⇒ この何気なくが大切なところ.本時の目当てを明示しなければとばかり,冒頭で「今日の目当ては,『三平方の定理を理解しよう』です」などとやったら喜劇かつ悲劇です.
推理小説を読もうとするとき,「犯人は〇だよ」と教えられるような感じですね.
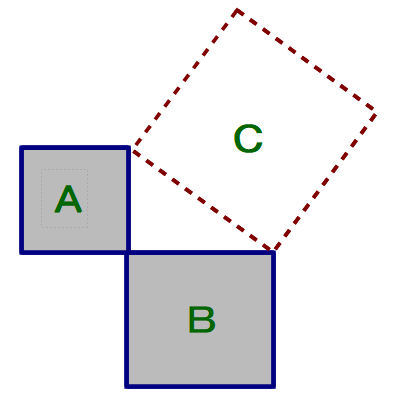
■ 「・・・上のような作図をして.正方形Cの1辺の長さを測ってCの面積を求めてください.正方形AとBの面積の和と(おおよそ)等しいはず.実は偶然ではないのです.約2500年前,古代ギリシア人のピタゴラスという数学者がいて・・・」(以下略)
このあと,三平方の定理の解説と証明に向かいます.
対辺の長さは対角と比例しないのか!
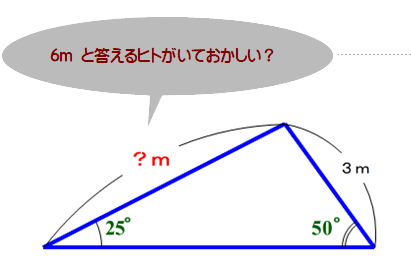
■ 上図で,50°の対辺の長さを6mと答えるヒト,いますよね.
もちろん,正解は正弦定理を用いて求めることになります.

■ 本問の場合,?をxとして,x/sin50°=3/sin25° より,x≓ 3×0.77/0.42=5.5(m)
■ 正弦定理ですが,a: b: c = sinA: sinB: sinC を押さえることが基本です.つまり,三角形において,各辺の長さは対角に比例せず,それらの正弦(sin)に比例するという確認です.
定理の2Rは比例定数ということになります.とにかく機械的に分母を払い,a=2RsinA, b=2RsinB, c=2RsinC とする光景を見掛けますが,本質から外れないようにしましょう.
■ 正弦定理に対するヒト3タイプです.

①数理感覚が優れており「対辺と対角は比例はしない」と元々認識しているヒト
②「対辺と対角は比例する・しない」を意識せずにいたが,上記例示と正弦定理により「しない」ことを認識したヒト
③ 上記ような例示もなく,正弦定理を学習した後も「対辺と対角は比例する・しない」が意識に上がらず,問題解きに走るヒト
⇒ ②タイプは①タイプまで伸びてほしいですね.さて③タイプです.数学的に価値あることに価値を感じない・・・.必ず壁に突き当たります.邪道ですが「テストに出題」はどうでしょう.ダメ元で挑戦しませんか.
■ ここまでは,導入時に留意するべき事例をあげました.次は,導入時以外でも”必要性”を確認するべき例を紹介します.
九九の暗記は必須です.しかし,

■ 九九の暗記は必須.それに異存はありません.ただ,九九を習ってしばらくした頃,しばしば見られる次のような実態があります.
■ 「6+6+6+6+6 と 5+5+5+5+5+5 ではどっちが大きい? 」
という質問に,何割かのヒト(子どもに限らず)は,実際にそれぞれ足し算をし始めます.
■ これは,6×5(or 5×6)の意味が徹底されないママ,九九を棒暗記しているからですね.
⇒ “六五三十”と言えたとしても,意味も分からず唱えているだけ?
6を5回も書き連ねるのはタイヘン ⇒ 6×5 と表す.
つまり,かけ算は足し算の連続使用で根っこは同じ.
確率計算で,乗法定理を習うと加法定理と混乱するヒトもいます.”本家は同一”という認識で当たってほしいですね.
<補足>
■ 「目当てを明示する」についてですが,その明示タイミングも重要です.授業の「冒頭で」とは限りません.冒頭もあるでしょうし,時には授業の最後でもよいかも知れませんね.要は,子どもたちの心理や心情をよく理解して適切な判断をすることです.
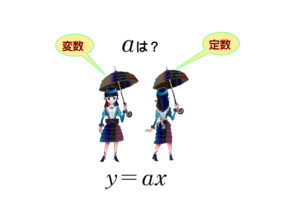
■ 次回テーマは,「定数か変数か」(予定)です.文字でつまずく一因に「定数なのか変数なのか,よく分からない」があります.思い当たる節も.一度整理してみましょう.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).