鈍角三角形面積 ⇒ Ｍさん(小学生)のナットク法

■ 三角形の面積公式は，s=ah÷2 (a:底辺の長さ，h:高さ) です．言うまでもなく鈍角三角形も含めての公式ですが，しっくりこない（釈然としない）ヒトもいるようです．

■ その違和感なり不安感の大元は，高さが底辺から離れていることにありませんか？

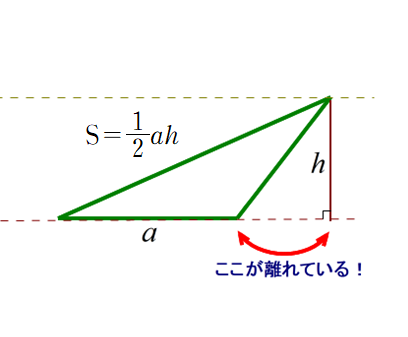
■ 数年前，山形県の小学生Ｍさんの自由研究作品と出会いました（「算数・数学の自由研究コンクール」理数教育研究所主催）．残念ながら全国審査まで届きませんでしたが，教科書にある公式に正面から向き合った印象に残る作品でした（※近年は，統計的な調査や観察に関する作品が多くなり，やや食傷気味です．私見）．

等積変形のくり返し

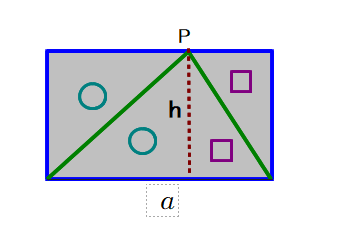
■ 上図は，鋭角三角形の面積が長方形の面積の1/2であることを示しています．公式 S=ah÷2 の背景がよく見えますね．

■ 次は，鈍角三角形の「等積変形」です．

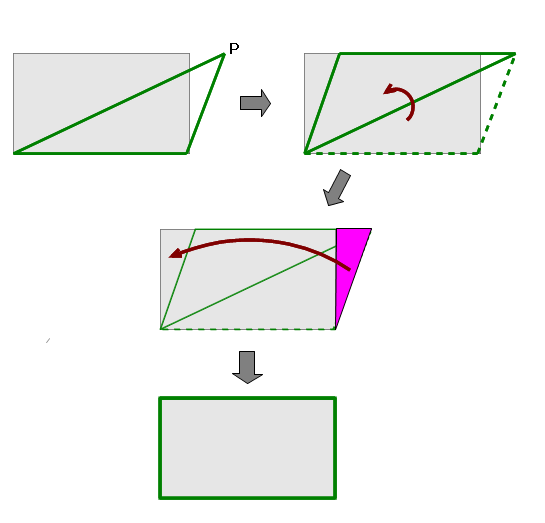
■ 最初の鈍角三角形に，折り返し等の変形をすることで，長方形の出来上がりが分かります．結局，公式 S=ah÷2 にたどり着きました．

長～く伸びた鈍角三角形でもいいの？

■ しかし，Ｍさんの問題意識は続きます．先ほどの鈍角三角形は，頂点Ｐが比較的長方形に近いので，折り返しも１回で済みました．でも，鈍角三角形にはいろいろなタイプがあります．極端に尖った鈍角三角形でも面積公式は同じだろうか，とＭさんは疑問を抱いたワケです．

■ 確かに教科書では，”平凡な”鈍角三角形を例に挙げて公式を導いていて，”とんがり度の強い”鈍角三角形は扱っていません．そこで，Ｍさんは次のような図を描いて自身へのナットク度を高めています．

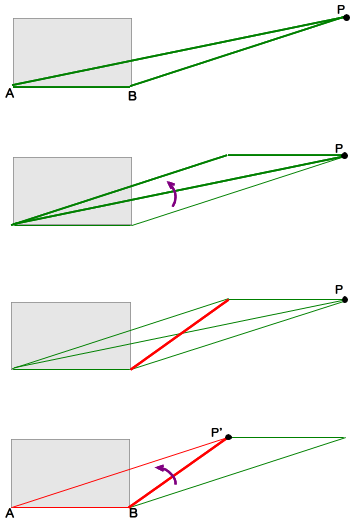
■ 最初の△PABが等積変形して△P’ABになることが分かりますね．頂点P’がかなり長方形側に移ってきて，とんがり度も弱まりました．この作業を必要に応じてくり返せば，いずれ証明の済んでいる”平凡な”鈍角三角形になります．

Ｍさんの感想

■ Ｍさんの感想（一部）

「･･･この公式が好きになりました．すべての三角形に通用する式を考えた人はすごいなと思いました」

■ この「すべての」という個所が本テーマの本質です．それに迫った小学生Ｍさんの問題意識（こだわり）に敬意を表します．算数・数学を学んでいく上で，意味あるこだわり感をもつことは，極めて意義深いことです．学年・年齢は関係ありませんね．

■ 本稿について，Ｍさん手書きの図など，作品自体をソノママ紹介したかったのですが，時もかなり経過しており，承諾手続きが現実的でないことから，Ｍさんの考え方を踏まえた内容にいたしました．

こだわり感あれこれ

■ 遠藤章博士（高脂血症治療薬スタチンの発見で，ラスカー賞，日本国際賞等受賞）は，東北の田舎（失礼）のお生まれです．幼い頃，キノコのハエトリシメジが”ハエには毒で，人間が食べると美味しい”様子を身近に見たことが不思議でならず，そのこだわりが現在に至る研究に繋がっていると語っています．

■ 世の中に余裕がなくなったため，あるいは，共通マークテストの点数アップに専念させるため，日本のあちらこちらで「貴重なこだわり」をスルーさせていないのかと，不安を感ずる昨今です．

 

   ※ 秋田魁新報 遠藤博士顕彰碑設置の記事(21.5.2)

 

＜補足＞

■ 次回テーマは，「0.999･･･=1 ?」（予定）で，悩む・悩まされる問の筆頭格です．定義？公理？定理？･･･そもそもこれらの疑問が「出る」自体おかしいのか？一緒に悩みましょう．

■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左，次:右).