θ と sinθ の大小
唐突な問いかけで「?」かも知れませんが,ある超重要定理ナットクへの”0.1歩”として話題に挙げました.
■ その定理(以下,超定理)とは
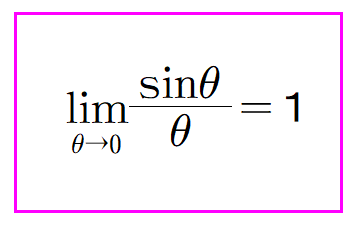
のことですが,登場する場面の多さ&広さ&深さが超定理の重要性を示しています.
それもあってか,証明自体はサラッと流され,「ホラ,またこの定理が使われるよ」と論が展開され,同時に計算問題も次々と紹介されていく現状が散見できます.
■ ここでは,息継ぎをするべく,算数や中学数学とのつながりに留意しながら証明自体に注目してみましょう.後々に役立つことを確約します.
Q1 次の不等式が成り立つ理由を説明してください.
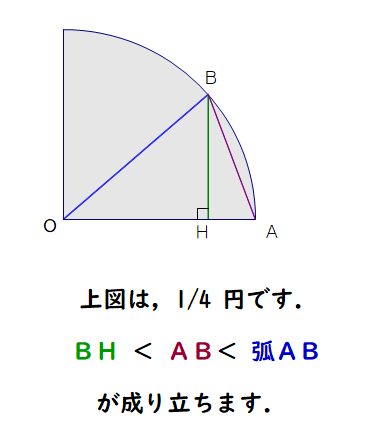
A1 ① AB<弧AB について
点AからBへ向かう道のりでは線分ABが最短コースになるからです(遠回りの法則).
② BH<AB について
△BHAにおいて,∠A < ∠H(=90°)なので,対辺BH<AB となります.
← 三角形における対角と対辺の大小関係の一致(証明はラク)
← この結果を「図から明らか」とするのはやや乱暴
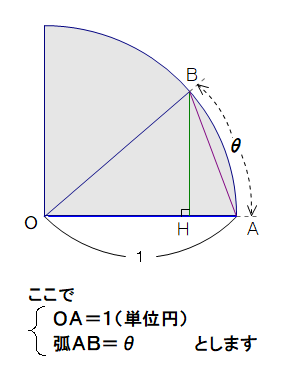
Q2 図のように
OA=1, 弧AB=θ
と置いたとき,∠BOH, BH をθを用いて表しなさい.
A2 次のようになります.
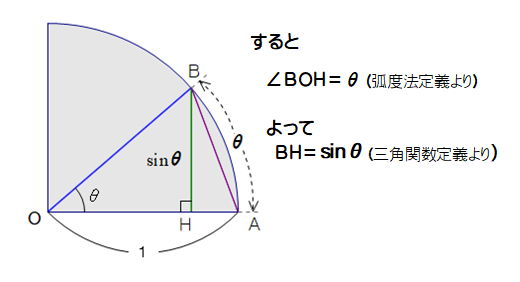
■ ∠BOH=θ についてですが,抵抗感をもつヒト,かなりいると見ております.いかがですか?
これは,弧度法そのものズバリです.つまり,弧度法とは,
中心角 ⇔ 弧の長さ
として,角に, 対応する弧の長さ をそのママ当てはめる約束のことです(⇔を=にする).
例:90°= π/2(単位円の1/4円周の弧長≓1.57).
よって,180°=π(≓3.14), 1°=π/180(≓0.0175)
※ これまでは,角といえば分度器で測るものと思い込んできたヒト,πといえば円周率であって角とは無縁と思い込んできたヒトには辛い発想の転換になりますね.これからは,
3.14 を見たら角180°を,3 を見たら角180°弱を
イメージしなければなりません. 弧度法については後日テーマで取りあげる予定です.
■ BH=sinθ について
三角関数(三角比含む)の正弦(sin)の定義によります.
■ 以上まとめますと
BH<AB<弧AB より,BH<弧AB つまり,
sinθ < θ
となります.
Q3 θ=1° のとき,sinθとθの値を比較しなさい.
A3
$$θ=1°(60分法)=\frac{π}{180}(弧度法)より$$
$$ θ=\frac{π}{180}=0.017453…$$
$$ sinθ= 0.017452…$$
小数点以下5位までは一致していることが分かります.
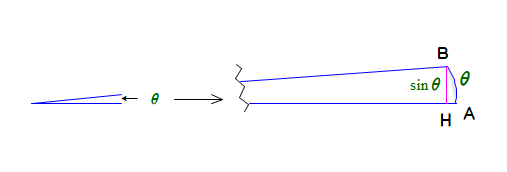
■ ここで,θ>0 かつ 十分小さいとします.
⇒ 図で,BHと弧AB がかなり接近する
⇒ sinθ<θ であるが,sinθ≓θ ※ が成り立ちそうです(かなり重要な結果で理工学では必須).
■ ※より
$$sinθ≓θ ∴ \frac{sinθ}{θ}≓1 $$
これで,冒頭の超定理の形に近づきました(次回に続く).
<補足>
■ 通常,扇形と三角形の面積の大小比較から,はさみ撃ちの原理で超定理を解説します.ただ,面積比較→曲線・線分の長さ比較 という発想は結構シンドイので,超定理の前半だけは面積を使用せず解説しました.
■ 次回のテーマは「θとsinθの大小(その2)」(予定)です.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).