やっちゃえ!”外分”
内分は特に問題はないとしても,外分となるとガラリと様相が変わるのは,今も昔も同じようです.一体何が…

■ つい先日も,twitter上で外分の質問を見つけました.それもほぼ定義そのもののような内容で「昔と同じ.全然カイゼンされていない!」との思いを強くしたところです.
外分のどこが難しいのか
■ 要因をいくつか挙げます.
(1) 外分点が正しく打てない(作図軽視の傾向?)
⇒ 定義がナットク感を持って伝わっていない
(2) 外分公式に登場する文字が多い
⇒ x₁,x₂,y₁,y₂,m,n の6文字(添数が苦手のヒトいます)
(3) 外分公式で –記号が気になる
(4) 内分点に比して,外分点には不自然さがある
まず,分点を打つルールから
■ 数学における点の打ち方には,内分・外分点だけでなく,チェバやメネラウスの定理でも共通するルール(暗黙の数学ルール!)があります.
⇒ 点を打つ際,ペン先は用紙から離れない ということ(スタートからゴールまで).
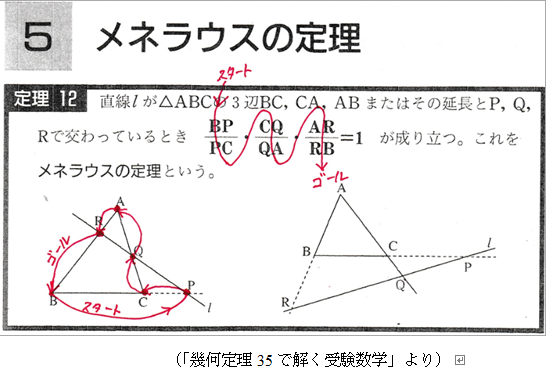
■ メネラウスの定理で説明します.ペンは,点Bからスタートして,P→C→Q→…→R→B と各点を打っていきますが,その間,ペン先は用紙から離れることなくゴールBまで動きます.
■ 次のⅠ~Ⅲの図で点の打ち方ルールを確認しましょう.
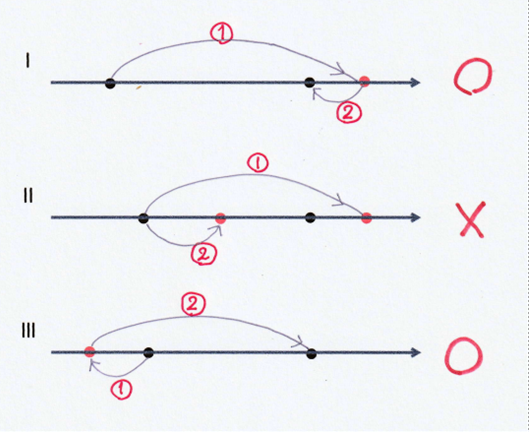
Ⅰ,Ⅲ は外分点を打っています.
Ⅱは,①の後,ペン先が用紙から一旦離れて②へと動いていますので,ルール違反ということになります.
実際に,外分点を打ってみる!
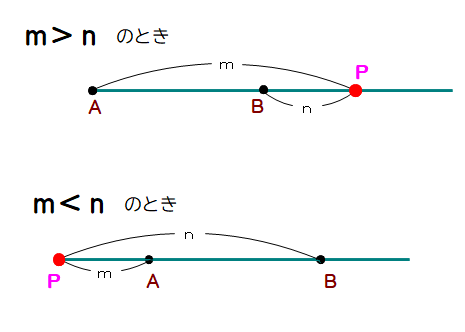
■ 線分ABをm:n の比に外分する点がPです.
<留意点>
①外分点Pは,線分AB上にはない ← もし線分AB上にあれば,それは内分点
②点Aがスタート,点Bがゴール(AからBを見る)
③m<n のときは,PはAについてBと反対側に存在
特に,③に抵抗感が強いようです.
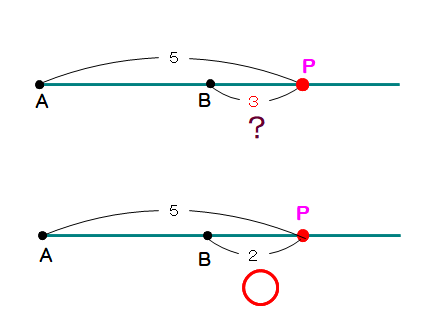
■ 左図上は,5:3 の外分点の例ですが,間隔が不正確過ぎ,BP=3 には見えませんね.
左図下は,5:2 の外分点でまずまずOKです.
■ ほぼ正しく外分点を打つのはそんなに簡単ではなく,ケッコウ苦労します.
<簡便法>
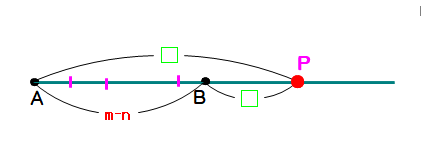
下図で,線分ABを(mーn)等分して区切りマークをつける(m,nは互いに素)
⇒ これにより,おおよそ正しい外分点が求まります
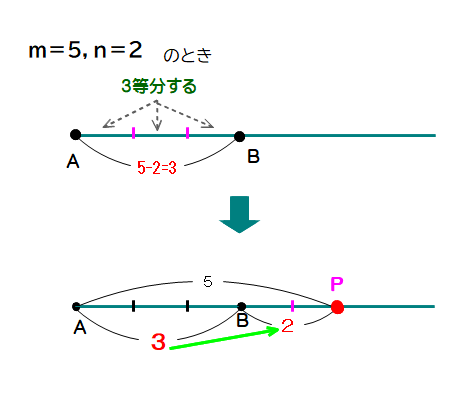
例 5:2 外分の場合
① 5-2= 3 ですから,線分ABをだいたい3等分する
② その2っ分でPを定めると,BP=2 となり,実際,AP=5 を満たす
※ m<n のときも同じような発想で柔軟に対応しましょう.
外分公式に親しむ
■ 結論から言うと,外分公式は,内分公式と一体的に解釈できます.
⇒ 覚えるべき公式が減ります!


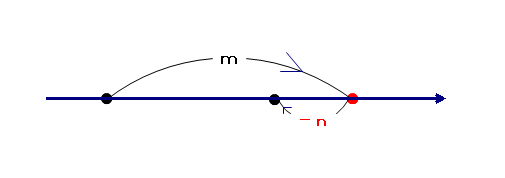
■ 上記外分公式変形からの逆発想になります.
① 線分ABに向きを与え,「A→B」を正の向きとする
② m:n の外分で,m>n ならば ,nに対応箇所が負の向きになると解釈できるので
内分公式で n → -n
の置き換えをすれば,機械的に外分公式が導かれます.
■ さらに,m<n のときは,向きから「–m:n の内分」と解釈でき,次の左辺のような式で表せます.この際,分母分子に(-1)をかけて
$$\frac{-mx₂+nx₁}{-m+n}=\frac{mx₂-nx₁}{m-n}$$
となります.
したがって,m>n, m<n のいずれの場合も
m:nの外分 ⇔ m:(-n) の内分
という解釈で,内分公式一本でコトが足りることになります.
<補足>
■ 次回テーマは「ベン図をキレイに書く」(予定)です.3つの円まではスムーズに書けますが4つの円はどうでしょう.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).