ベン図を4つの円で描く?
ベン図は集合の範囲の見える化に必須のツールです.その際,円3つまではスイスイと描けるのですが,4つ以上となると…
4集合のベン図
■ 下図は,集合A, B, C に,何とか集合Dを付け足したものです.
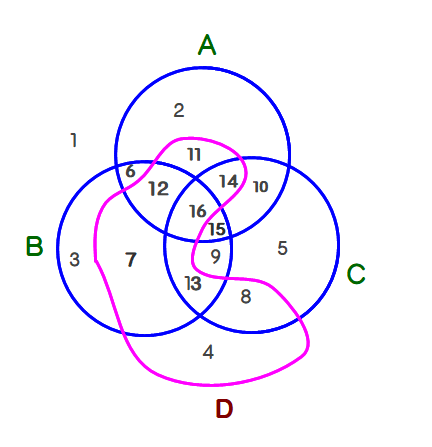
■ 「何とか」としたワケは,円3つで8部分(領域)に分かれていたところに
8つの各領域ごと,集合Dのメンバーで{ある,ない}の判断をする
つまり
4つ目の集合Dでもって,すべての領域を2分割しながら描く
必要があったからです.平面を2⁴=16分割することになり,実際,やってみるとケッコウ手間のかかる作業です.
■ この集合Dのベン図をシンプルにしたいものです.
集合Dを円で描けないか?
■ 試行錯誤的にやってみると,円で描くのは困難であり,不可能だろうと予想できます.さて,どう説明しますか?
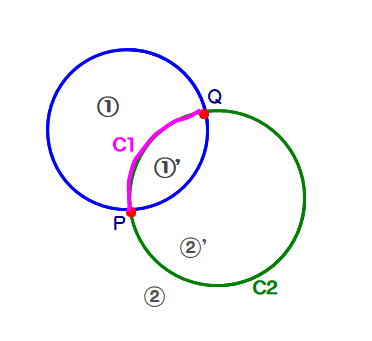
■ 図は,青円によって平面が①②の2つに分かれているところに,緑円を付け加えた様子です.
2つの円により,2交点P, Q ができる.
⇒ 円弧C1(短), C2(長) ができる
⇒ C1により,①’ が出現
⇒ C2により,②’ が出現
結局,2交点により,2領域が増えることになります.
■ 本題に戻ります.3つの円でベン図は8領域に分かれています.
そこへ4つ目の円Dを付け加えます.
⇒ Dは各円とそれぞれ2交点持つ
⇒ すると,2領域ずつ増え,計6領域増える
⇒ トータルで8+6=14 領域となる
⇒ これは,4集合による領域は16(=2⁴)であることに反する
よって,ベン図として4つ目の円は描くことができないことが分かります.

■ 上述は背理法による解説で,論理としては分かるにしても,どこかスッキリしないと思いませんか(背理法の宿命?).
そこで,集合自体に絡ませず,単純に図形(幾何)問題として挑戦してみましょう.
背理法によらない解説
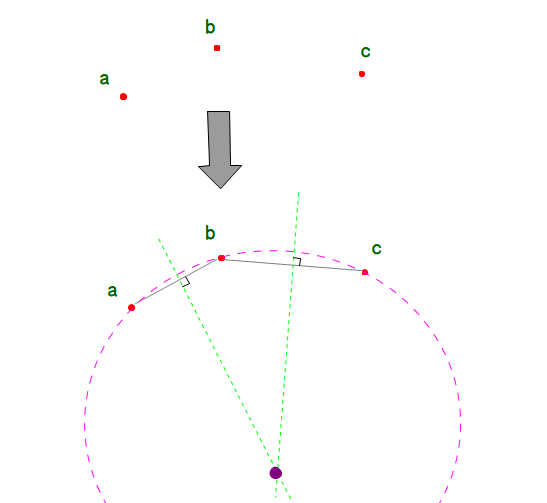
■ 図のように,一直線上にない3点を通る円はただ一つ存在します.
・2線分の垂直2等分線の交点がその円の中心となります.
・あるいは,座標を導入して円の方程式:x²+y²+ax+by+c=0 とします.
3点の座標数値を代入して,連立3元方程式を解くと,a,b,c が求まる!
この解説でもokですね.
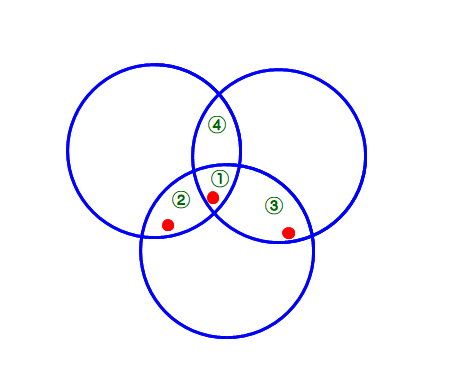
■ 上図で,書き足す4番目の円Dは,各領域を必ず通過します.そこで,①②③の各領域から適当に3点(赤)を選び,円Dが3点を通るとします.
図の場合,3点を通る円は一通りに決まりますが,上に凸(円の上半分)の状態であり,その円が上方の④の領域は通過できません.
※点の取り方により下に凸にもできますが,その場合もやはり通過できない領域が下方に発生します.
同様にして,他の領域から3点を選んでも,やはり通過できない領域が現れます.
<まとめ>
4つの集合からなるベン図を,4つの円で書き表すことはできない
<補足>
■ ベン図を円で描いたとき,円と円の位置関係が決定的で,円の大きさは不問であることは言うまでもありませんね.
■ 次回テーマは「sin,cos,tan って何?」です(予定).三角関数アレルギー発生源に,この記号も含まれているようです.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


