sin って何?
三角関数(含む三角比)にある程度慣れた頃に,フト疑問を持つヒトがいます.「sin って何?」と.
最近も次のような質問をtwitter上で見つけました.
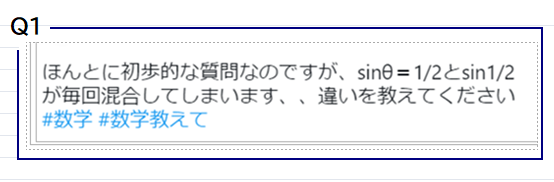

■ 質問の主旨は
$sinθ=\frac{1}{2}\ $
$と$$sin\frac{1}{2}\ をしばしば混同してしまう$
ということのようです.
■ 次のように“正しい”説明する数学リーダーもいます.
前者:三角方程式で,0°≦θ≦180°ならば,θ=30°,150°
後者:(弧度法が未履修として)まったく意味ない式
基本に戻って三角比の定義を見直すべし!!
■ 確かに”そのとおり”なのですが,投稿者とどこか噛み合っていません.
twitter上でのやり取り

↓ sin1/2 について

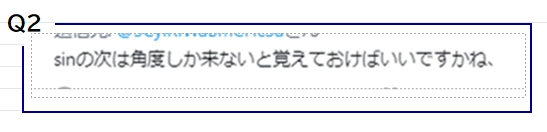

“再認識”は重要です!
■ 投稿者は”sinの次は,角が来る”と改めて認識をしたようです.
⇒ こういった“再認識”は,飛躍のための重要なステップになります.
× sin1/2=150° × cos√3/2=30° 〇 tan45°=1
■ ”sinの次は,角が来る”ことを数学的に捉えましょう.
sin, cos, tan は( ?)記号です!
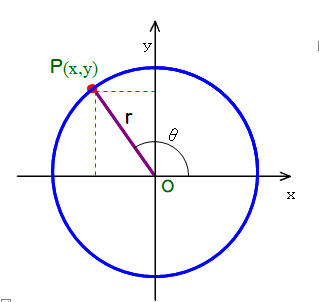
■ 左図は,原点中心半径rの円と,円周上の1点P(x,y)を表し, ∠POX=θ です.
■ すべての円は相似ですから
$$比 \frac{y}{r},\frac{x}{r}, \frac{y}{x} の値は,rと無関係,θのみで決まります.$$
⇒ つまり,θの関数 です!
$そこで, \frac{y}{r}=f(θ), \frac{x}{r}=g(θ), \frac{y}{x}=h(θ) $
と仮置きします.
■ ただ,f( ),g( ),h( )は他の領域でもよく使用されている関数記号ですので,三角関数「占有」とすることはムリな話.
そこで,三角関数独自の関数記号を編み出すことにしました.
⇒ f → sin , g → cos , h → tan とします.
⇒ f(θ)=sin(θ) ですが,カッコは不要ということで,sinθ としました.cosθ,tanθ も同様.
※ sin の語源 ← sinusoid(正弦曲線) ← sinus(曲線:ラテン語)
<マトメ>
sin は, 角の関数記号である.よって,sin の次には角が書かれる.cos, tan も同様.
<補足>
■ sinθ を初めて紹介する際,「この式は,s×i×n×θ ではありません」と念を押す必要はないかも知れませんが,日々使用する語句や記号に鈍感な数学リーダーが結構いますよ.無理数なんてどう説明しますか?(※ 無理数は誤訳の典型.本来は,無比数)
■ 次回テーマは「お飾りか?積分定数」です(予定).
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).