1当たりの大きさ…1って何?
「算数つまずき」の一つ.まず1(単位量)がわかりにくい.自然数の出だしの数なのですが,扱いには苦労します.

■ 代表的な問があります.
Q1
$\frac{3}{4}m²の壁を\frac{5}{8}dl で塗れるペンキがあります.$
$このペンキ1dlで何m²塗れますか.$
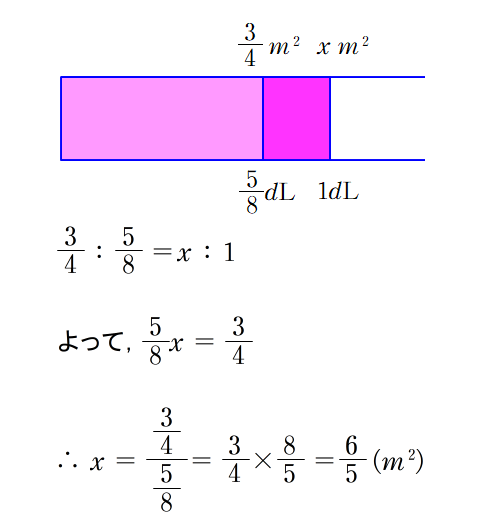
A1 面積と使用するペンキ量は比例すると考えて,図のように比例式を立てると
面積 x=6/5 (m²) と求まります.が,正答率はあまりよろしくありません.
さらに 3/4÷5/8 が
1当たりの大きさ
を求める計算を示している,という解説が付くと余計にワケがわからなくなったりします.
■ この”1当たりの大きさ“について,①ナットク感があるか,②他のヒトへの説明ができるか,という視点で考えてみましょう.計算はできるが,理由はよくわからない典型例かも.
日常生活でよく目にする量
■ 小学低学年児童は,普通「3桁の自然数123」の意味理解はしていないはずです(10進法未学習なので).でも,123円の買い物はできるものです.
この事実は,金銭のやり取りなど身近な生活経験が未学習分野の理解をサポートする例を示しています.

■ そこで,1当たりの大きさのナットクのため,日常生活数理の活用を試みましょう.
■ 量にもいろいろなタイプがあります.
長さ,重さ,時間 等…基本量(単位は m, g 等)
面積,体積 等…基本量の組み立て(単位は m², m³ 等)
速さ,密度 等…基準となる量との比(単位は km/h, 人/km² 等)
速さ・・・”1当たりの大きさ” の典型例
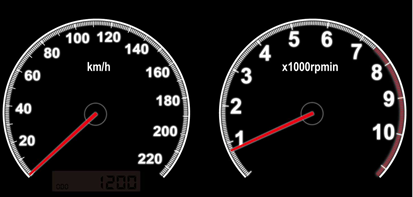
■ 1時間に50km走った車の速さを
50km/h と書き,時速50kmと言います.
この単位記号:km/h に注目しましょう.
km/h … km:距離,/:割算(÷), h:時間(hour,60分) を示します.
厳密に書けば,1km, 1h(60分) ですが,1は省きます.
同様に,秒速10mの短距離ランナーの速さは,10 m/sec と書きます(sec:秒).
■ 3時間で150kmを走った車の速さは,150km÷3h=50 km/h ですね.
⇒ km/h は計算式自体をそのママ反映しているわかりやすい記号です!
⇒ km/h は小学校高学年あたりから日常で目にすることも多いでしょう.10進法理解における金銭計算と同じで,これを利用しない手はありません.

■ 上の例から
1時間当たり or 1秒間当たり ⇒ 1当たりの大きさ
と具体例をもって理解することで,ナットク感は深まります.
単位記号 km/h のフル活用
■ 計算式をそのママ反映している記号として,km/h などを挙げました.
さらなる活用を考えましょう.

■ 悩ましい”1当たりの大きさ”ですが,「フツー150/3 は3で約分して即50とします.分母分子にわざわざ1/3を掛けるとはしませんよ」.その通りなのですが,その際は50/1 ではなく,単に50 と書きますね.
つまり,”1当たり”が見えなくなります.分母が1 になるように式変形をするという機械的プロセスに注目させたいものです.
Q1 (冒頭の問です)
$\frac{3}{4}m²の壁を\frac{5}{8}dl で塗れるペンキがあります.$
$このペンキ1dlで何m²塗れますか.$
A1’
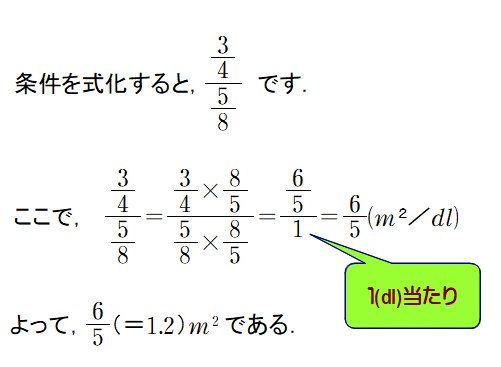
<補足>
■ 次回テーマは「マークシート方式の功罪.特に罪」です(予定).新年度ですのでマークについて「再確認」をします.
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.

≪…分母が1 になるように式変形をするという機械的プロセス…≫を、円の等分割で[見える化]するのはどうでしょう・・・
≪…(3/4)m ²の壁を(5/8)㎗で塗れるペンキ…≫を、
[(6/8)m ²の壁を(5/8)㎗で塗れるペンキ]と分母を(8)で纏めて、
円(1m ²)の8等分割の6個分(m ²)と円(1㎗)の8等分割の5個分(㎗)で眺めて、
円の8分割を外(8倍)して、
[(6)m ²の壁を(5)㎗で塗れるペンキ]となります。
≪…このペンキ1㎗で何²塗れますか…≫は、[ペンキ1単位(㎗)で何m²塗れますか]となり、
[ペンキの1m ²あたりの消費(必要量)の単位を創る(分母の意味(5))を捉える。]ことになる。
≪…よって、6/5(=1.2m ²)である。…≫
とするのはどうでしょう。
≪…1(㎗)当たり…≫を、[円の8分割を外(8倍)して]と円の分割の通分で眺め、分数割り算をエジプト分数的に観る。
√6 様へ
コメントありがとうございます.
ご指摘のように「…分母が1になるように式変形をするという機械的プロセス…」が本稿の要です.
が,その肝心要のところで「機械的プロセス」という言葉で「逃げてしまった」思いをずっと持ち続けていました.
今回の√6様の解説で雲が晴れたような気がします.
2分数の通分から2円の等分で論を進める方法はすべての場合に適用できますのでナットク感は高いと考えます.
重ねて感謝申し上げます.
※いろいろな場面で紹介させてください.