部屋割り論法がここで登場する
「n個の部屋に(n+1)以上の客を泊めようとすると,相部屋(2人以上の客が入る)が必ずできる」という体験を基にした原理が”部屋割り論法”ですね.引き出し論法,鳩ノ巣原理とも言います.

■ ネーミングからしてもわかりやすい原理であり,学習者のナットク感は高いです.しかし実際の適用場面となるとシックリ感は今一つということもありそうです.その原因を探ってみます.
部屋割り論法 は相部屋の”存在だけ”を示す原理
■ 部屋割り論法は,相部屋が何号室であるかは示しておらず,ただ,相部屋が必ずあることを主張しているのです.
例1 生徒が367人います.このとき,同じ誕生日である生徒が少なくとも1組はいます.
⇒ 同じ誕生日である生徒名を挙げることはできませんが,必ずいるという存在保証をしています.
例2 分数1/7を小数展開すると,循環する無限小数となります.
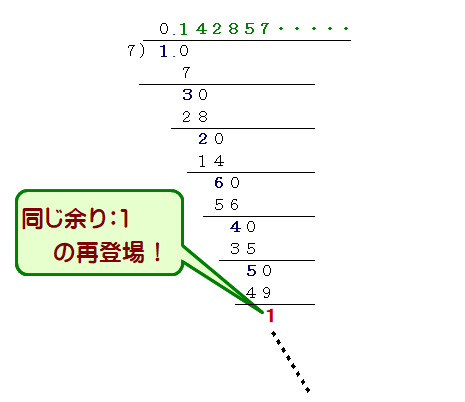
⇒ 図のように7で割算を続けますと,余りは{ 0,1,…,6 }のいずれかです.一方,1/7は無限小数ですから(※),余りは0以外の6とおりです.
6とおりの場合(部屋)に,延々と続く割算回数を当てはめるワケですから,割算7回目までには必ず同じ余りと会うことになります.そこから前回と同じ商が続き,以下くり返しが続きますので循環小数となります.
※ 1/7が無限小数となるワケは,本blog”1/7にまつわる問題あれこれ“を参照ください.
■ 存在 という言葉の響きが固く,日常生活では用いることがほとんどありません.もはや国語や数学,公民等の”教科書用語”かも知れません.
“存在”とは?
■ n次方程式の解の公式(係数dataで解を求める手順を示す計算式のこと)について
① 2次~4次方程式までの方程式:それぞれ解の公式があり,解を求める手順が示され,同時に解の存在も示されている.
② 5次(以上)方程式:解は存在するが,解を求める手順を示すことができない(ガロア理論).
■ ある子どもは小6で140cm, 中1で155cmの身長だったという.
このとき,小6から中1の間で身長がジャスト150cmとなる瞬間があったはず(中間値の定理).
⇒ その日時・時刻はわからないものの,瞬間は存在したはず
⇒ 言い換えると,150cmという値をジャンプして成長することはできない!
部屋割り論法 がフル活躍

Q 自然数がp個並んでいます.この中からいくつかの数を選ぶとその和がpの倍数となるものが少なくとも1組はあります(存在します).なぜでしょう
例1 { 15, 7, 100, 3, 49, 11 }
⇒ p=6, 15+7+3+11=36 ok!
例2 { 2, 11, 4, 67, 19 }
⇒ p=5, 11+4=15 ok! 2+11+67=80 ok!
A p=5 の場合で考える.
自然数を{ n₁,n₂,n₃,n₄,n₅ }として
a₀=0, a₁=n₁ ,a₂=n₁+n₂ , a₃=n₁+n₂+n₃, a₄=n₁+n₂+n₃+n₄, a₅=n₁+n₂+n₃+n₄+n₅ とおく.
a₀~a₅ の計6個それぞれを5で割ったときの余りは,{ 0,1,2,3,4 }のいずれかである.
すると,部屋割り論法によりa₀~a₅の中に5で割ったときの余りが等しいものがある.
仮に,a₂とa₅だとしよう.すると,a₅-a₂ は5の倍数ということになる.
つまり,a₅-a₂=(n₁+n₂+n₃+n₄+n₅)-(n₁+n₂)
=n₃+n₄+n₅ が5の倍数!
他の場合も同様に説明できる.証明終
<補足>
■ 部屋割り論法は「”数”の話」(啓林館,船越俊介氏)を参考にしました.
■ 次回テーマは「奥深い3進法」です(予定).
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.