3進法と天びん
2進法はコンピューターと”一心同体”の記数法であり,10進法は日常生活に不可欠な記数法です.その点,3進法は存在感が薄いのですが,天びんと絡ませると教材としておもしろい結果が出てきます.
3進法の例
■ ある自然数xが3進法で20212(3) と表されているとします.
※ここで,20212を二万二百十二 とは読まず,に/ゼロ/に/いち/に が普通の読み方
■ 20212(3)を10進法で示すと
x=2・3⁴+0・3³+2・3²+1・3¹+2
=185(10) であり
3進法5桁の数 x=a₄a₃a₂a₁a₀ (3)は
x=a₄・3⁴+a₃・3³+a₂・3²+a₁・3+a₀・1 (10)
です(各ai=0,1,2).5桁以外の数(→任意の自然数すべて)も同様のルールで構成されます.
⇒ 3進法では各桁で用いる数は{0,1,2}のいずれか.例えば234(3)という3進法表記はありえません.
Q1 197を3進法で表しなさい.
A1 図のように各商を3で割算し続けて求めた余りを⑤→①の順に書き表せばよいのです.
197(10)=21022(3)

※ 上図で①②が求まるワケ
197= …+27a₃+9a₂+3a₁+a₀
=3(…+9a₃+3a₂+a₁)+a₀ ⑥
∴ a₀は197を3で割ったときの余りであるから,a₀=2 ①
次にa₁に狙いを定めよう.
⑥でカッコ内は65になるので
65=…+9a₃+3a₂+a₁
=3(…+3a₃+a₂)+a₁
∴ a₁は65を3で割ったときの余りであるから,a₁=2 ②
以下,③④⑤も同様の計算で定まる.pointは後ろの係数a₀から求めることですね.
⇒ これらの一連の計算を簡素化したのが図の筆算になります
3進法に制限をかけましょう
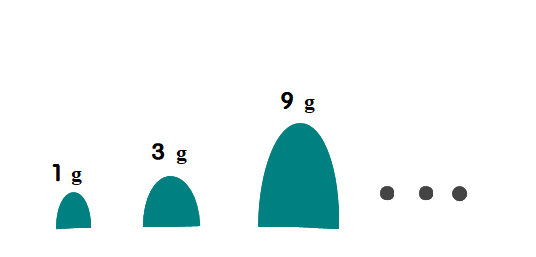
■ 図のように,1g, 3g, 9g, 27g…のおもりが1個ずつあります.
Q2 これらのおもりを使って表すことのできる重さを小さい順に7つ書きなさい.ただし,使わないおもりがあってもよいとします.
A2 x=a₀+3a₁+9a₂+27a₃+… を満たすxを求めればよい.ただし,各係数ai (i=0,1,2,3…)= 0 or 1 である.小さい順に7つ書き連ねると
x=1, 3, 4, 9,10,12,13
※ 各”おもり”が2個ずつ用意されていれば,通常の3進法に相当するのですべての重さを表記できます.
おもりと天びん
■ 重さが不明の物体Pがあります.天びんとおもりを用いた測定ルール(以下,天びん3進法という)は次のようです.
① 1g, 3g, 9g, 27g…のおもりを各1個ずつ用意する.
② 天びんの左右の皿におもりとPを適当に選んで載せ,天びんを釣り合わせてPの重さを測る
この方法でどんなPの重さ(1g単位)も測れることを示しましょう.
例えば,25gの重さは次の図のようにセットすればよいのです.
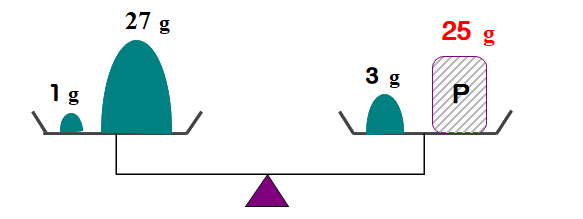
Q3 天びん3進法で46gを測りなさい.
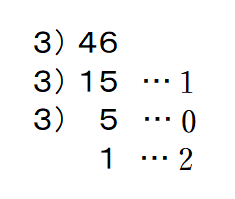
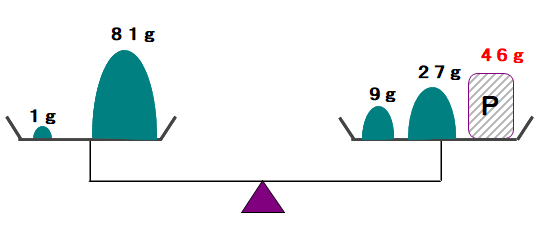
A3 図のように p=46(10)=1201(3) です.
以下,3進法で表すと
p=1201
=1000+200+1 ①
①で各おもりはせいぜい1個のみですから,200 を何とかしなければいけません.
ここで,200=1000-100ですので (← 18=27-9)
①=1000+(1000-100)+1
=2000-100+1
ここで,2000=10000-1000 より
p=10000-1000-100+1
∴ p+1000+100=10000+1
したがって,1+81=27+9+p
ゆえに,天びんがバランスをとれたときのpの重さは46g であることが分かる.
Q4 すべての自然数(物体Pの重さ)は天びん3進法を用いて表すことができる.そのワケを述べなさい.
A4 任意の数pを3進法で表したとき,
①各桁の数が{0 or 1}の場合(例:p=11001(3)),すべてのおもりを天びんの皿に載せれば,逆の皿でバランスが取れたときの重さがpとなる.
②各桁の数の中に2が入っていたとき(例:p=2021(3))
2000=10000-1000 ← 54=81-27
20=100-10 ← 6=9-3
のように2を用いない同値変形をすることで,すべての桁から2を除外できる.そして-のついた数を移項(pを載せた皿へ移動)すれば天びんのバランスが取れpを測定できる.
例:p=61(10)=2021(3)
=2000+20+1
=10000-1000+(100-10)+1
∴ p+1000+10=10000+100+1
p+27+3=81+9+1

Q5 天びん3進法による重さpの測定の仕方は1通りに限定されます.なぜでしょう.
例:46は,{1,81}と{9,27,46}の分け方以外にはない(Q3参照)
A5 理屈がやや長くなります.

<補足>
■ 天びんバランスによる測定ですが,3進法だけ(2進法は”移項”が生じない)の特徴で,実際,5進法などでは成立しません.
■ 次回のテーマは「見当をつける力」です(予定).思考する場合は当然として,計算する・させる場合も見当をつける力&習慣が大切です.
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.