1/7 にまつわる問題あれこれ
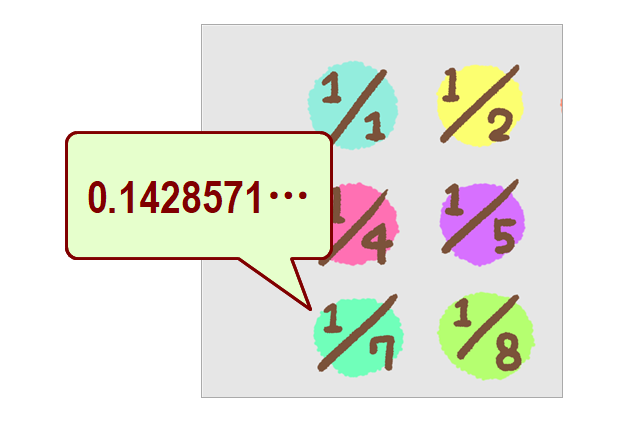
有理数1/7 はある意味で分数の「代表」です.a=1/7にまつわる問をいくつか挙げます.
Q1 aを小数に直しなさい Q2 b=0.142857…を分数に直しなさい Q3 aが循環小数となる理由を述べなさい Q4 その他(「a=1/7のイメージを描きなさい」)
Q1:割算が延々と続きます.
Q2:巧妙な式変形で求められますが,無限に続く数のかけ算や引き算をするので数学的には疑問符が付きます.正式には無限等比級数の和の公式(高数Ⅲ)を用います.
Q4:かつて熊本の小6生T君は1/7を例に分数をイメージ化し,同年自由研究作品コンクールで文部科学大臣賞を受章しました(本blog”学習の進んだ子供“に掲載).
ここでは Q3 (循環小数になるワケ)を掘り下げてみましょう.
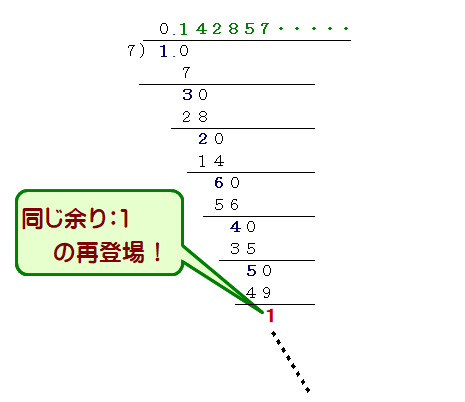
■ 図のように分母7で余りを次々と割っていきますが,余りrは{0,1,2,3,4,5,6}のいずれかになります(r=0のときは有限小数).
なぜ r≧7 とならないか? ⇒ (背理法を”軽く”用います)もしr≧7ならば,正しく割り算がなされていない,つまり商としてもっと大きい数がたっていたはず.割り算で除数(この場合は7)以上の余りが出るはずがない!
■ 1/7が有限小数とならないワケ(※1)は後述しますが,小数展開が無限に続き,余りsが 1~6 のいずれかであるとすれば,割り算7回目までにはsと同じ余りが必ず登場する(※2)ことになります.
■ したがって,1/7の場合はそれまでの商142857が小数点以下に延々と続くことになります.
1/7 が有限小数とならないワケ(※1)

■ なお,有理数αが有限小数となる必要十分条件は,「αを既約分数で表したとき,分母の素因数が2と5のみとなること」です.
\[ 例 \frac{3}{2・5・5}=\frac{3}{50}=0.06 \] \[ 反例\frac{8}{3・5}=\frac{8}{15}=0.5333・・・ \]<補足>
■ ※2「sと同じ余りが必ず登場する(※2)」についてですが,「部屋割り論法」の原理が根底にあります.「n部屋に(n+1)人の客を入れようとすると,少なくとも1部屋には複数の客が泊まることになる」という内容です.
■ 次回テーマも部屋割り論法を話題にします(予定).
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.