“外積の大きさ” ⇒ なにか違和感が…
空間ベクトルa,bに対して,外積:a×bとは次の性質をもつベクトルのことです.①a,bと垂直,②a×bの大きさ(長さ)はa,bのなす平行四辺形の面積を表す

■ 外積をイメージしようとするとき,①はともかく,②で戸惑うヒトおりませんか?
■ 定義|a×b|=|a||b|sinθ で,右辺は図の平行四辺形の面積を示しています.ただ,ベクトルの長さOP=面積 とは??という(一瞬抱く)違和感です.
■ 面積や長さ,時間等々の量を数量化したものをスカラーといいます.難しそうな言い方ですが,向きのない量という意味で,普通の実数としてよいでしょう.
y軸でスカラーの大きさを視覚化
■ 図は都道府県の面積を示した棒グラフです.数学の視点でいえば,面積というスカラーを棒の長さ(これもスカラー)に比例対応させることで,各都道府県の広さの違いが一目瞭然となっています.
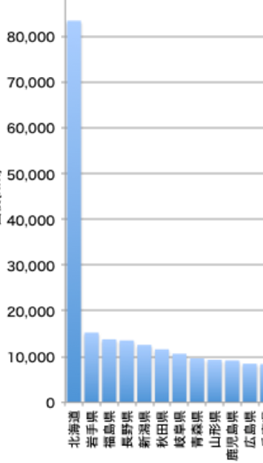
■ 例えば,岩手県の面積は約15,000km²で,その値をy軸方向の長さ(高さ)で示しています.
■ 小学校の社会や理科の教科書を開くと,多くのページでカラフルなグラフが目に入ります.一般社会でも人口や各種経済指標,温度変化等々の理解・解説にはグラフが不可欠です.
⇒ 外積a×bのルール「向き:a,bの張る平行四辺形と垂直,長さ:a,bの張る平行四辺形の面積」と本質的には同じ!
外積 a×b の向き&尺度
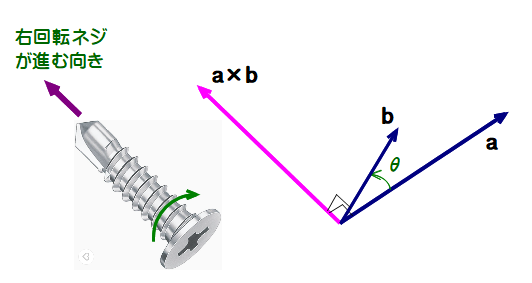
■ 外積a×bについて
(1) 向き
aからbへ向かう角をθとするとき,外積の向きは,右ねじが進む向きに一致します(定義).
(2) 尺度
通常のグラフではy軸の1目盛りの長さは扱う対象により適宜尺度を変えます(例:都道府県の面積では90,000km²を上限にして目盛りを付けている).
ところが外積の場合,a,b, a×bとも同一3次元空間のベクトルであるので,a×bの向きだけ尺度を変えることは不可能です.
つまり,外積を図示しようとする場合,1辺1の立方体(内部含む)を無数に集めた空間におけるベクトルとなります.
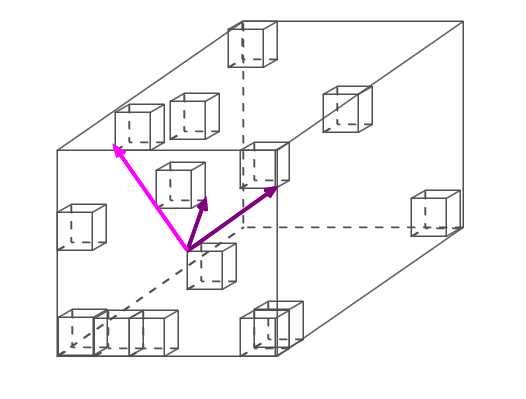
<補足>
■ 内積,外積とも「天下り式」の定義から進みますので,何かと抵抗感は強いモノがあります.小学校社会科教科書を例に挙げましたが,数学のリーダーは「他教科の活用」にも目を光らせたいものです.
■ 次回テーマは「出題の工夫」(予定)です.「テストから授業カイゼンを図る」は昨今の学テや共通テストをみて感じますね.
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.