残念な”即,計算”
「算数・数学 ≓ 計算 」①と理解しているヒトはかなりおります.もちろん①を全否定はしませんが,即,計算に走る・ダッシュする姿には大いなる疑問を感じます.算数・数学の学びを単に「公式に当てはめ○をもらうこと」にミスリードしているのではないか?という懸念です. ⇒ 一つのカイゼン策が「計算前の見当付け」です.
気になる授業光景から
■ 授業や報告等でしばしば見かける光景
(1) 「25.3÷2.3 を計算しなさい」
<展開例>
① 「まず5分間,自分だけでやってください.答えはタブレットに電子ペンで書くように」
② 「答えがいろいろ出てきましたね.1.1 か 11 が多いね.では15分間,各班ごとに考え方と答えを求めていきましょう」 (以下略)
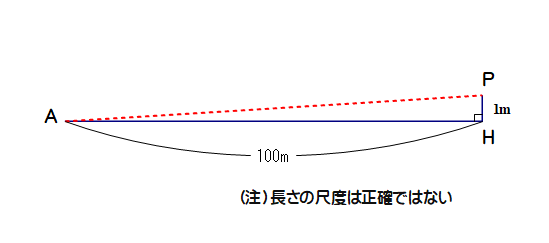
(2) 図のように,100mトラックのゴール上に身長1mの子どもが立っています.スタート点をA,子どもの頭をPとしたとき,APの長さを求めなさい.
<展開例>
① 「重要な定理を使いますよ.5分間自分の力で解いてください」
② 「白紙のヒトが結構いますね.答えが出たヒトもいますので,各班で話し合ってください」(以下略)
(3) 「野球で3割バッターがある試合で3打数1安打する確率を求めなさい」

<展開例>
「独立試行の例です.公式に当てはめると,₃C₁(1/3)¹(2/3)² となるので……」(以下略)
何が”残念”か
■ ①②は昨今よく見かけるパターン化した授業展開であり,③は典型的な一方通行の授業展開です.
3例共通して思考を伴わない計算に陥っていると言わざるを得ません.
思考の一つ:見当を付ける
■ 思考力を深めることを目標にしながら,上に挙げた3例は,結果として思考力を削ぐ授業展開となっています.カイゼン展開例を紹介します.
例(1) 「25.3÷2.3 を計算しなさい」
「すぐ計算できるヒトもいますね.でもチョット待って.だいたいどれぐらいになりそうかな」(中略)
「11か12くらいですか.〇さん,どう考えたのか紹介して」(中略)
「△さん,今までのやり取りを参考にして,答えが1.1とか110にはならないワケを言ってみて」
(中略)
「では5分間,自分で計算して答えをタブレットに書いてください」(中略)
「各班ごとに10分間話し合って正解を求めてください」
「各班ごと似たような問題を作って,さっきのようにおよその値をメンバー全員で確認してから計算を進めてください」(以下略)
<参考>令和4年度 全国学力学習状況調査 算数

※ 全国正解率:34.9%
■ 4択ですから当てずっぽうでも25%程度は正解となります.それを加味すると事態はより深刻です.中には,これは算数以前の読解力の弱さだと指摘する向きもありますが,国語等の他教科の役割を言及しても生産性はゼロです.
⇒ 一般市民からすれば, 算数の学びを通して読解力を身に付けよう という姿勢が支持されるでしょう.
例(2) 図のように,100mトラックのゴール上に身長1mの子どもが立っています.スタート点をA,子どもの頭をPとしたとき,APの長さを求めなさい.

■ 中には,100m+1m より101mとする学習者が必ずいますが(大人も含めて),これこそ「歓迎すべき間違い」です.
⇒ △PAHにおいて,AP<AH+PH が成り立つことを再確認できる絶好のチャンス
■ 三平方の定理を用いてAP=√10001 となりますが,それで「了」とすることはこの教材が可哀想です.
AP=√10001 を求める前に次のような問いかけを!
⇒ 「ところで,斜辺APと底辺AH(=100m)との差はどれくらいだと思う?これから計算でAPを求めますが,その前におよその見当を付けてください」
AP<101 より差は1m未満だと分かりますが,さてどの程度でしょう?50cmくらい,20cmくらい,10cmくらい,あるいはそれ以下?


■ 最低限,電卓を使用して√10001≓100.005 を求めさせて,差:5mm までは確認したいものです.違いがたった5mmしかない!ことに驚く学習者がいるはず ← このためには見当を付けることが不可欠
「答えが合った!○をもらった」とは次元の異なる心の動きに価値があります.このような数学リーダーの姿勢の有無は1週間程度ならともかく,年間単位で考えるとその差は取り返しのつかない違いとなります.
■ 中学の範囲を越えますが,学習の進んだ子どもを念頭に,上記の分子の有理化にも触れたいものです(有理化の意味&意義が理解できる).教育の機会均等とは「全員同じゴールを目指す< 全員それぞれの伸びを保障する」ものと考えます.
例(3) 「野球で3割バッターがある試合で3打数1安打する確率を求めなさい」

■ 本問の題意がはっきりしない学習者は少なからずおります.おそらく半数以上かと.
■ 確率を求める際,予想をさせることで題意が伝わることがあります.
大いにあり得るのか,ほとんどないのか,あるいは半分程度なのか.
本問は格好の例です.
⇒ 「3割バッターはこれまで平均して10回打席に立って3本はヒットを打ってきたなかなかの選手.その選手が3打席で1本ヒットを打つことってどのくらいありそう?(大いにある,まずない,半分程度).さてどうでしょう」
■ 題意を理解するには,身近な例で状況が確認できればベストですね.3割バッターは強打者・巧打者です.その選手が3打数1安打する・・・これはアリだね,という思考判断です.
ところが答えは,₃C₁(1/3)(2/3)²≓0.444=44.4%です.これは予想と比してやや「意外」な数ですね.ホントかいな?と解答を見直したりすることが,学ぶ意欲や学力の向上につながります.
その際,活動スタイルは,個人でも班でもよいわけで,「学び合いが大切だから必ず集団でなければならない」という論には疑問を感じます.活動スタイルは手段であって目的ではありません.
<補足>
■ 「計算あって思考なし」は陥りやすい指導法です.
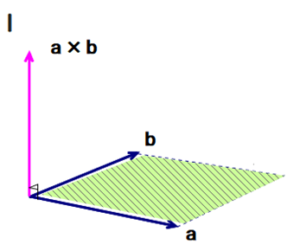
■ 次回テーマは「外積」(予定)です.内積と外積:ネーミングは近いのですが・・・
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.