テスト問題のカイゼン
全国学力学習状況調査問題と大学共通テスト問題(以下,学テ等)を拝見すると,出題者(国)⇒ 算数・数学リーダー への強烈なメッセージを感じます.

■ すなわち「この問に応じた授業展開をしてね・するべし!」という方向明示です.
※ 昨今,学テ等では1問が数ページにも渡る「大河ドラマ的長編」形式が定着した観がありますが,これについては後日テーマにする予定で,本blogでは小問をメインにしています.
「指導カイゼン」に絞る

■ 定期テストをはじめテスト実施の目的は何でしょう?
⇒ 子ども自身が学びの状況を確認する,指導要領資料・調査書の基礎データにする等々の意義がありますが,ここでは
算数・数学リーダーの指導カイゼンにつなげる
ための実施である,と目的を絞ります.
例1 全国学テ算数から
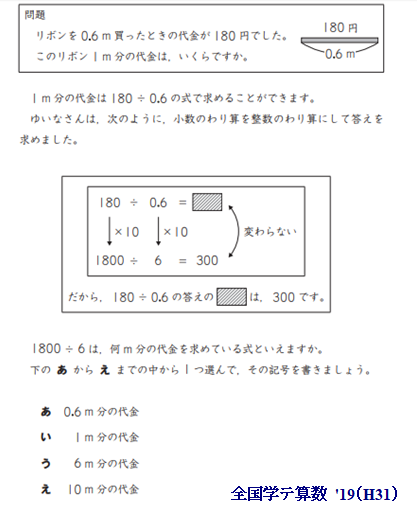
■ いわゆる1単位当たりの量という領域の典型問題で,小学校算数の中で子ども&数学リーダー双方が扱いにケッコウ手こずっています.
正解は「い」で正答率47%ですが,4択であること,問題リード文にも「1m分の代金」と明記されていることを合わせ考えると,真の理解度は3割台かと.
<本問の特色>
①あらかじめ答は300円と示されている
②計算プロセスからその数の意味するところを問う
という内容です(定期テスト等ではなかなかお目にかからない).
つまり,仮に,正しく計算できているとしても,理解して計算しているのかどうかチェック可能な問いかけとなっています(→ ただ,4択は少なすぎです!).
学習者の個々の顔を思い浮かべながら次の指導に活かせる内容です.
一般論ですが,今も昔も子どもは敏感です.テストに出ないと見越すとその学びに力は入らないことも現実ですので参考になります.
・・・・・・・・・・・・・・・・・・・・
例2 式の計算

■ 分数式前の符号は式全体にかかる,という基本ルールがなかなか徹底できない状況があります.
ドリル学習を重ねてそのときはナットクしても元に戻ってしまう例が多々あり,本問もその仲間.
■ Q’ は テスト中の学び を期待しています.テスト中の集中度は普段の授業とは格段に異なるもの.その集中力を利用しない手はありません.
(1)で2つの式の違いが注意が向かいますね.中には迷うヒトもいます.その迷いが次のステップに繋がります.
そのプロセスを経て(2)に向かいます.
結局×となった学習者に対しても,解決に向けたヒントを伝え得る問になっています.
・・・・・・・・・・・・・・・・・・・・・・・・・
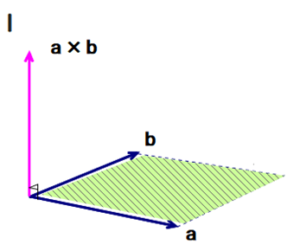
例3 微分計算
■ 微分計算自体は「苦」ではありません.なぜなら計算ルールが単純だからです.しかし,意味理解を伴っているかとなると話はベツです.
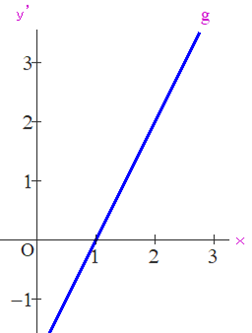
Q 左図はxy’図であり,直線gは,yの導関数:y’=2x-2 を表しています.このとき元の関数:y=f(x) の概形をフリーハンドで描きなさい.
■ y=x² ① のとき,y’=2x ② であり楽勝ですね.しかし,①上の任意の点P(x,y)における接線の傾きが 2x で示されているという認識はどうでしょうか?
本問では,y’=2x-2 の場合です.
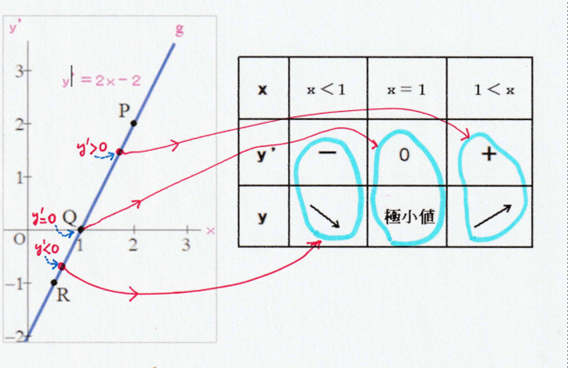
■ 左図のように
y’=2x-2 のグラフ ⇔ 増減表
がタイアップしています.
y’の値=接線の傾き という認識がないとこのタイアップが理解できません.
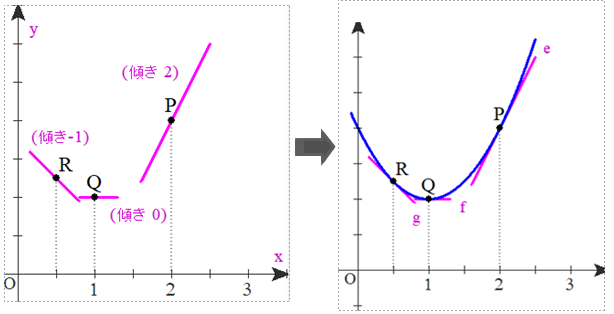
A フリーハンドで描いてみました.y=f(x)の定数項(C)は不明ですので,C=2 ぐらいとしています.
※ 積分すると,y=x²-2x+C
点Qが最下点になることの読み取りがpointです(最下点でないと.上の増減表は作成不可).
<補足>
■ 上記作問3例については,採点基準があいまい,印刷が難しい,数学科内の了承が難しい,採点時間がかかる等々のハードルもあるでしょう.その際ですが,すべての判断基準を無意識のうちにマークシート方式に置いていないでしょうか?
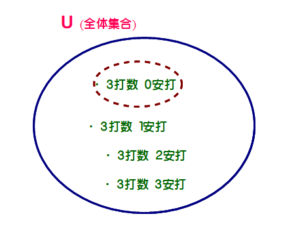
■ 次回テーマは「『少なくとも』がピンとこない…」(予定)です.分かるヒトにとっては何でコレが問題になるの?でしょうが.
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.