低すぎる濃度正答率21.6%(全国学テ)

大学共通テストと同様，全国学テ出題形式の潮流が”長文＆大河ドラマ”的となりました．その是非は別として，算数で個別にみると 濃度 が深刻です．

■ 本文を拡大します．

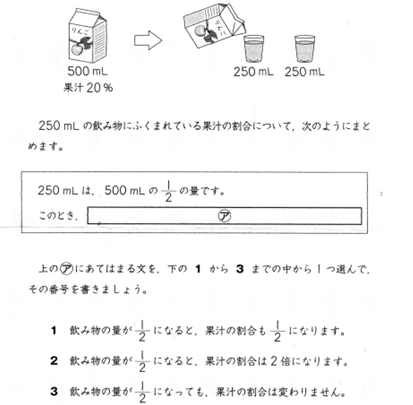
■ 正解は当然３ですが，この正答率は 21.6％（全国）．

総量が1/2になっても果汁の割合（濃度）は変化しないという判断は，学校制度がない時代から（いやはるか大昔から）日常体験により備わっていたであろう生活必須の能力です．

日常の具体場面と授業

■ この生活体験がなぜ教室の学びには反映されないのか？

古くは「路上の算数」（street mathematics※）と形容された課題と軌を一にしていますね．

※ある途上国では子どもも商売の大事な担い手．彼らは路上で様々なモノを販売して，合計やお釣り計算など瞬時に行うことが多いとのことです．しかし，その彼らですが，教室内で算数テストとなるとからきしダメで，昼見せていた鋭い計算力はスッカリ姿を消しているという事例．

カイゼンへの第一歩

⇒ この 体験と教室の断絶を数学リーダーがまず認識・自覚すること

そこを踏まえて個々に「作戦」を練り上げるしかありません．

昨今「個別最適＆協働学び」を発することが流行になっている観がありますが，発して”終わり・思考停止” となっているケースも散見されます．

その崇高な理念に基づく具体の取組みを注視している昨今です．

読解力不足だ！との声

■ 「これは算数（数学）云々ではなく，それ以前の”読解力不足“にこそ原因がある！」という声も聞こえています．

しかし，本blogでも指摘してきましたが，暗に国語など他教科に責めを求める姿勢は間違いです．そんなグチを何時間吐いても解決には1mmも進みません．

読解力は，すべての教科・教科外活動で意識的に取り組むべき総合力です．算数を学びながら読解力を付けましょう．

HR活動や部活動に取り組みながら読解力も向上できます．実際，すぐれた部活動指導者の言は，概して論理的で説得力に富み，読解力upに繋がっていると見てきました．

それにしても21.6%は低すぎ！

■ 濃度問題は，過去にも全国学テ（’12 中理など）で出題されています．

■ 標準解答は「食塩が水に溶ける量には限りがあるから」で正答率：48.3%です．

小中・教科の違いはありますが，比較して前述の算数濃度正答率：21.6％の異様な低さが気になります．

特に，本濃度問題について算数は3択マーク式，中理は記述式であることに留意すると（マーク式は記述式に比して得点は高い傾向），一層理解に苦しむ結果です．

出題形式に疑問

■ 冒頭でも触れましたが，昨今，国実施主体のテスト（小中高）が「大河ドラマ」的構成となりました

⇒ 問題リード文の超・長文化 

⇒ 本濃度問題も“たどり着く前に憔悴しきった”子どもの表情が容易に想像できます．

「正解のない時代，状況を読み取る力こそ必要だ」とばかり，国主催テストを，マーク式かつ長編モノ一色にして与え続ける…どういう結果を産み出すのでしょうか．

■ くり返しますが，21.6%という数値は異常かつ異様です．

濃度は味見などの例から

生活数理上の確認　→　その一般化

という流れで決してハードルの高い問ではないのに，ゴールする前の「行き倒れ旅人」化した子どもたちがかなり多かったのではと思います．

■ さらに，マーク式出題はそもそも「選択肢の消去法」を解法の定石とせざるを得ず，出題形式としても疑問がある中「３択はないでしょ！」ということです．

でたらめに選んでも33.3%の正答率，それでいて21.6%の正答率はどう分析したらよいのか・・・．

確かに痛いところを突いている良問ですので，中理でやったように記述させる方がベターでしたね．子どもは自身の考えをより率直に考え，自分の言葉で表現したと思います．

選択肢は「出題者の思考」です．子どもは自身の思考と合わせながら再構築しなければならないので思考の邪魔という側面もありますから． 

＜補足＞

■ フランスの大学入学者試験問題（バカロレア）では「哲学」が文理問わず課せられ，’23では「平和を求めることは，正義を求めることか？」がテーマの一つで試験時間は4時間．問題文：一行とは！

マーク式の対極にありますね． ・・・日本が失ったモノの代償は計り知れないかも．

■ 次回テーマは「問いかけの必然性」（予定）です．授業の流れを決定付ける珠玉の問を！

■ にほんブログ村ランキング（数学教育）にかかわってバナー↓のclickをお願いします（宣伝が多く恐縮です）．