「めあて⇒先生のめあて」を散見しますが…
いつの頃からか「”めあて”の明記」(※)が声高に叫ばれようになりました.そして(※)が伝言ゲームよろしく「めあての明記は授業冒頭で行う」のように変質を遂げた場面にも遭遇しました.これでは(※)の理念なりが,ガチガチの画一的授業形態主義に陥っているというべきです.

■ ガチガチでなくとも「めあての明記」が強調されすぎた結果,めあて自体に疑問を抱くこともあります
⇒ 例:何の脈絡もなく突如「~することができる」などと板書(それも大書で)されると,引いてしまう子どもも少なからずいるのでは?
⇒ 子どものめあてというより,先生のめあて化しています
めあてにつながる「必然性」に注目
■ 中高の数学ではむろんのこと,算数であっても1単元くらいの範囲では「論理の流れ・つながり」を意識した授業展開がなされるべきです.
“めあて” 様相
<かけ算>・・・めあて2例
Ⅰ 今日のめあてはここに書めましたが「かけ算をおぼえよう」です.まず・・・(以下略)
⇒ 率直に言って「×」ですね.推理小説を読もうとするヒトに「この小説で犯人は〇〇ですので,そこをしっかり押さえて読んでください」と助言するような印象すら覚えます.
Ⅱ 〇さん,ペンケースに鉛筆何本入っていますか?
5本ね.■さんは?4本ですか.
1班と2班で7人いますね.全員5本ずつ持っているとします.
すると,全部で何本になりますか?どんな式になるかな?
5+5+5+5+5+5+5 (※) ですね.答えは・・・ハイ,35本です.
ところで,(※)の式をどう思う?答えじゃなくて.
「長い」「同じ5しか出てこない」
そうそう.それでね,今日のめあては「式を短くかいてラクをしよう」です・・・(以下略)
⇒ 数学的にはややラフな感じもしますが,かけ算への流れ・必然性は低学年の子どもにも伝わると思います.
<三平方の定理>・・・めあて2例
Ⅰ 前回学んだ三平方の定理ですが,中学数学では横綱クラスの定理です.
ハイ,そこで今日のめあては「三平方定理の応用に挑戦しよう」です…(以下略)
⇒ 進度優先・教科書追従の授業スタイルでやはり△×ですね.これだったら冴えたyou tuberの方に軍配が上がります.
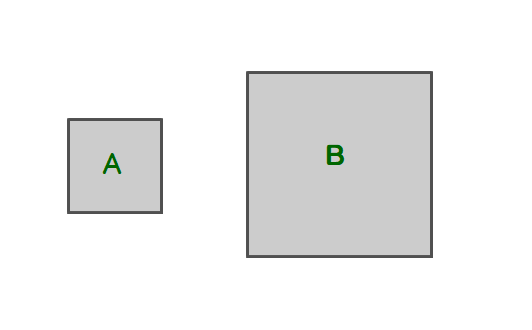
Ⅱ これは大小の正方形A,Bです.
面積がA+Bとなるような正方形Cを描いてください.
「それぞれの面積を教えてください」
不明です.図だけの提供です.
「作図しなさいということか」
そういうことになりそうだね・・・(以下略)
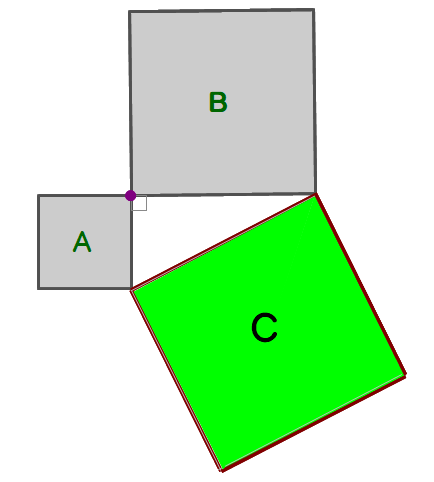
■ 図のように正方形Bを平行移動して真ん中辺りに直角三角形を誕生させると一気に解決に向かいますね.正に三平方の定理そのものです.
⇒ 本問いかけの方が「A+B=C を証明する」よりはるかに子どもの心情にフィットしています!
このあと,めあてを含めた展開に進みますが,本問の扱いは三平方の定理の応用よりも単元の1時限,つまり冒頭で登場させる手もありそうです.
■ 例:本問を投げかける→ 試行錯誤させる→ 解答を紹介(理由は抜きでよい)→ めあて「図形クイズに潜む重要定理を理解しよう」等を提示 → (以下略)
<補足>
■ 相手の「心情」に関心を持っての授業展開を!と常々思ってきました(思うだけで達せずじまいが大半でしたが).
■ 次回テーマは「重心の魅力」(予定)です.重心は,数学と物理を結び付ける強力な「心」です.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(昨今,宣伝が多く恐縮です).