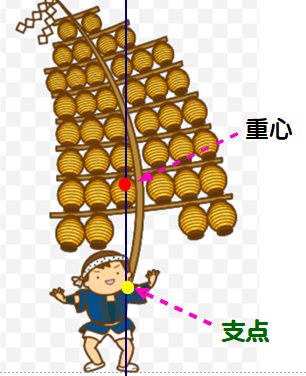
竿灯をコントロールできるワケ
竿灯を操る(名手の場合ですが)・・・重心が主役です.重心のイメージとして,①モノの重さが集中する1点,②ヤジロベエの支点のように全体バランスが取れる1点,③2中線の交点(三角形の場合)…などが挙げられましょうか.
■ この重心ですが,数学では高校での取り扱いとなります.しかし,イメージも含めて生活の中に十分浸透している実態があります.日常語としても「重心を少し前に!」など,スポーツ指導でもよく耳にします.
それゆえに 誤解 or 勘違い で終始しているケースもあるようです.
支点 = 重心?
■ 早とちりです.やはりヤジロベエのイメージが強烈なんですね.
重心 =その1点で全体をバランスよく支えることができる(支点)
しかし,この解釈は,①「狭っ!」②「誤解」です.
※ 重心の定義:物体or質量系において,各部分・各頂点にはたらく重力の合力の作用点(重力の中心)であり,質量中心と一致する.

①ドーナツですが,重心はどこにありますか?
直感的に「穴の真ん中」辺りですね.ヤジロベエのようにその1点で全体バランスをとるような操作は可能ですか.
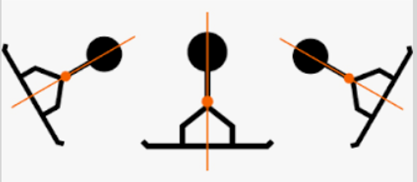
■ 物体に重心Gは存在します.ヤジロベエで考えてみましょう.
①Gは必ずしも物体の内部にあるとは限らない
②重心Gと支点Pはベツモノ
理由は次のとおりです.
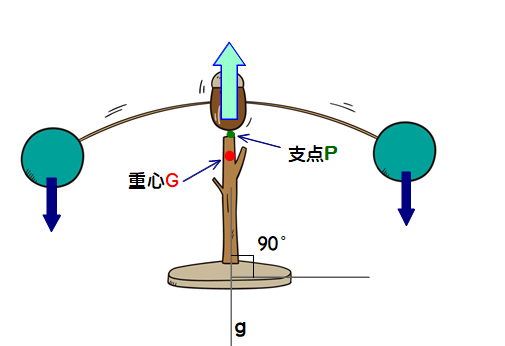
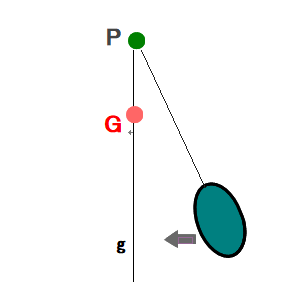
■ 上図で
①ヤジロベエ全体の重心Gは支点Pの下部にある
②支点Pはドングリの底部分にあり,全体の重さと釣り合う力で真上に押し返してバランスをとっている
③直線PGは地面に対して垂直である ← Pからの鉛直線gは必ずGを通る(※)の言い方が本質を突いていると思います
ヤジロベエが安定するワケ
■ 重心Gが支点Pの下部にあるとき,物体が安定するワケは何でしょう.
上図は,物体の重さは水色矢印の大きさで示され,支点Pで真上方向に押し返している様子でした.
■ ここで仮に右の重りが右上向きに少し動いたとしますと,右重りには鉛直線gに近づこうとする力が生じます.その結果,今度は反動で左重りが多少左上向きに動きますが,やはり左重りもgに近づこうと動きます.
この動作をくり返していきますが,全体の運動エネルギーは増加することはなく減少するので,次第に物体は鉛直の向きで静止しようとします.
つまり,安定!
実際,ヤジロベエでは,多少重りが動いても支点Pは”踏ん張って“バランスをとろうとしますね.
支点Pが安定 ⇒ P は動かしにくい点
■ ヤジロベエの動きから
支点が安定 ⇒ 物体の多少の変化では支点Pは”動じない” ⇒ 支点Pを動かすにはケッコウな労力が必要
以上を逆に考えると
支点Pが不安定 ⇒ Pは操作しやすい
■ 重心Gが支点Pの上にあるときは,ヤジロベエと上下反転の状態になり,支点Pは不安定 ⇒ P は動きやすくなる ⇒ Pは操作しやすい
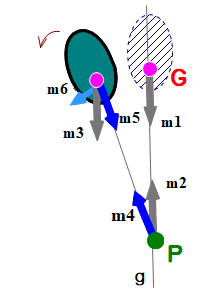
■ 図で,重りには真下への重さがかかっています.また,m1~m6 は,各矢線で示された力(=ベクトル)の大きさを表すとします.
重りをほんの少し左側へ傾けたとき(m6),ヤジロベエのように鉛直線gへ戻そうとする力は働きませんから,より左向きに倒れようとします.支点Pが動かなければ,重りはどんどん倒れ続けます.
← 通常のヤジロベエの場合は,PGが鉛直線上に並ぶよう力が働いていました.
■ 図でm1=m2=m3, m4=m5 であり,m3を平行四辺形による作図でm5とm6の和に分解していることから m3>m5 となります.
⇒ 支点Pにおける操作はより軽い力で行うことができる.
つまり,Pをより素早く動かすことで重心Gと支点Pが鉛直線上に並んで物体が安定するよう仕向けることができる.倒れる向きにハンドルを切ってバランスを取る自転車の原理と同じ.
⇒ 竿灯の妙技に繋がっている!
■ 以上振り返ると鉛直線g上に重心Gが存在する(※)という原理が決定的に効いてることが理解できます.より詳しい内容は,本blog”重心はなぜ一つか?“を訪問ください.
■ 次回テーマは「振り返り」(予定)です.振り返りによって「一段高いところに立つ」,そうありたいものです.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).