思考にも〇△が…
算数数学で課題を解くとき or 論を展開するとき，見方や考え方がフル回転しますが，最近，気になる（正直に言うと”気に障る”）ことが増えました．
■ 今日，教育界（学校）においては個別最適＆協働的な学び がキーワードになっていますが，後者：協働～に関連して画一的・形式的・予定調和的な場面と遭遇することが多々あり，やや閉口気味です．
諸々の考え方に即「いいね」は疑問
■ SNSの発展とともに「いいね文化」が列島を覆っており，この風潮が学校教育に与える影響もかなり大と考えています．
協働的な学び ⇒ 学び合い ⇒ 少人数による協議・・・という形態が確立しており，そこでは
メンバーの発言＆姿勢＞協議内容
となっている傾向が強くありませんか？
■ 協議内容を吟味するよりも，発言回数等による「活発さ」に価値を置き，ボード上の付箋カードの枚数（≓最大公約数）で結論を出しそれで「こと足れり」とする光景です．
授業においても同様で，課題に対してグループ協議で何らかの意見を発すれば進行役や周囲から「いいね」とされるような空気感です．
いろいろな考え方
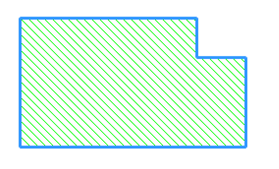
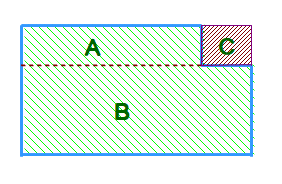
■ 図のように，長方形の1角が欠けたような図形の面積を求める場合，話し合い（協議）をさせるとどんな声が出るでしょう．
①底辺と平行線を引き長方形A,Bに分割してそれらを足す
②コーナーにある長方形Cを求め，全体（長方形）から引く
などが代表例でしょう．
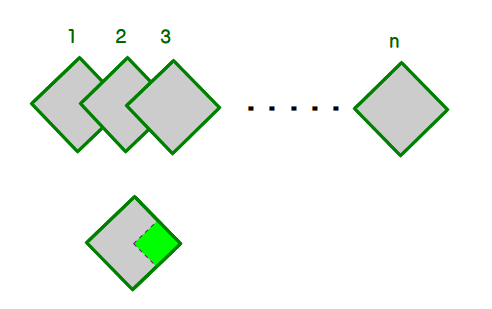
■ 図のようにn個の正方形が一直線状に並んでいます（正方形の中心に次の正方形の頂点を置く）．このとき，図形全体の面積を求めましょう．1辺の長さ10cmとします．話し合いはどうなるでしょうか．
下図で
①緑の正方形を除いたL字形の図形に注目し，それら(n-1)個の面積を合計して最後の一枚で調整する
②正方形の面積は100cm²．それらをn個加えて，緑の正方形(n-1)個の面積を除いていく
といった声が出そうですね．
■ 上の2例の場合，ともに①：分割，②：補充引去り という数学的考え方（思考）となります．それぞれナルホドと分かり差異はなく，それこそ「いいね」ですね．メデタシメデタシ！
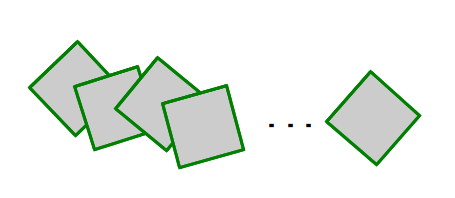
※ ところで，正方形の問で，頂点は中心点に置くが回転することもある，とすれば，全体の面積はどうなりますか？
思考にも〇△があり得る
■ 「みんなちがってみんないい」とは詩人金子みすゞの言葉（童謡）で人権尊重の原点です．しかし，数学的思考に「人権尊重」を形式的に当てはめることはエラーです．
より優れた思考を賞賛し，より価値を認めていくスタンスが社会の発展に繋がります．ガリレオ裁判が反例の象徴ですね．
⇒ いろいろな思考には優・良・可が付くのが通常で，「みな同列」はむしろ少ないと考えるべきです
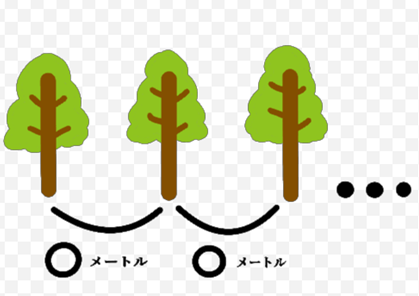
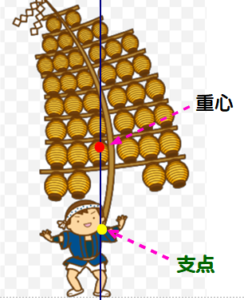
■ 図は「植木算」の説明を示しています．
例：木が3m等間隔で50本植えられているとき，端から端までの距離を求めなさい．
■ 大別して2通りの解法が予想されます．
＜解1＞①もし，木の本数が5本なら間隔数は4ヶ．10本なら9ヶ．このように，間隔数=木の本数-1 が成り立つので，本問の場合，間隔数は49ヶである．よって，求める距離は，49×3=147(m)
＜解2＞
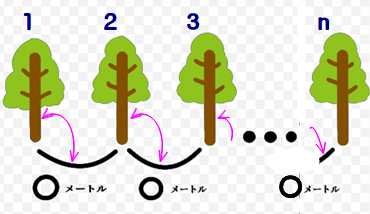
①図のように，それぞれの木と直下の間隔を対応させていく（お相手にする）．
②すると，最後の間隔は49番目の木が対応する．よって，求める距離は…（略）
＜解1と解2の比較＞
■ 正直，歴然たる差・天と地の差 があると考えます
⇒ そうか！どちらも「いいね」などとコメントすることは罪です！
もちろん，解2の発展性について解説すればよいので，解1にケチを付ける必要はなしです．
■ ＜解2＞の根源には
集合における 1対1対応 の思考があります．関数の本家です．
かつて，木下藤吉郎（秀吉）は信長から杉林の膨大な杉の木を数えよと命を受けましたが，かなりの速攻で応えたというエピソードがあります．
■ 解1と2の違いは何でしょう．
解1は，木と間隔を数えてその結果を比較して帰納的に，間隔数=木の本数-1 を導いています．
解2は，数える必要がなく対応付けをして，最後の過不足の様子から結果を求めています．
■ 秀吉の話ですが，家来たちはヒモを十分用意して，そのヒモを各杉の木に1本ずつ縛り付けます．終了後，すべてのヒモを回収して全体本数を専門家がカウントして信長に伝えたワケです．
当時は漢数字の時代で，今日のようなアラビア数字は存在しておらず数千に及ぶ数詞とは一般庶民は縁がありませんでした．しかし，
⇒ 木とヒモの 1対応1
の思考で，信長の無理難題をかわしたワケです．
■ 遡って原始時代，ヒトのリーダーは属するグループに対して，獲物や実をどうやって分配したのでしょうか．一般のヒトは公平さをどのようにナットクしたのでしょうか．
1対1 の手渡し・手配りがまず考えられる方法ですね．数詞を知る必要はありませんから
⇒ 数詞の誕生ははるかに後のことで 1対1 は数詞に先行すること数千年かと
＜まとめ＞
■ 問や課題に対して
Ⅰ 答が求まればよく，それまでの思考過程は第二義だという姿勢には賛同できません．公式棒暗記主義に直結します．
入試があるじゃないか！→ 入試を超える「対策」を構築したいもの
Ⅱ 発展性ある思考Aについては，①Aを見逃すことなく適切にフォローする ②（可能ならば）Aを用いて一段上の課題に挑戦する・させる
⇒ ①②を通して，Aの持つポテンシャルを改めて再認識する・させる
最後に次の問に挑戦しましょう．
Q 下図のように長方形が319ヶ（たて11ヶ, 横29ヶ）長方形上に並んでいます．対角線PQを引くと，PQは長方形をいくつ通過しますか？
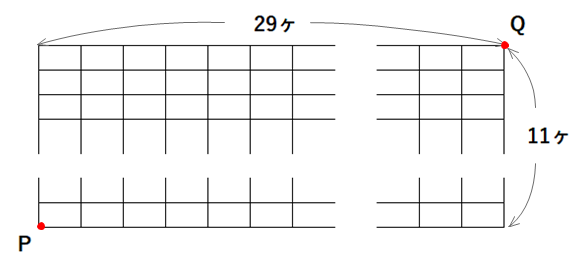
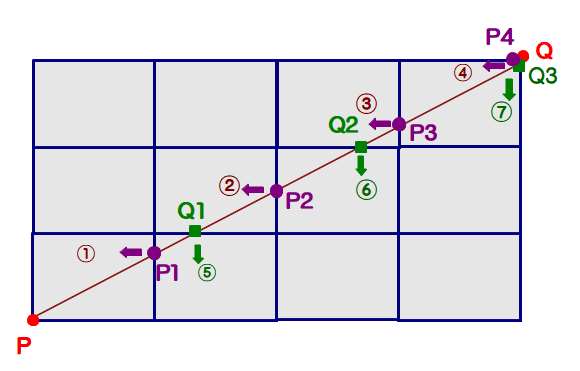
A 左図のような3×4 の長方形12ヶの場合で考えてみます．
■ Pを出発した対角線は縦線4本と交点P1～P4をもちます．
その際，対角線が通過した左側の長方形を順に①～④とします．
P1 → ① ～ P4 → ④
つまり，各交点と各長方形との1対1対応です．
■ 次にPを出発した対角線は横線3本と交点Q1～Q3をもちます．
その際，対角線が通過した下側の長方形を順に⑤～⑦とします．
Q1 → ⑤ ～ Q3 → ⑦
これも各交点と各長方形との 1対応1 です．
以上のことから，通過長方形は，①～⑦ですが，④と⑦がダブルカウントされているので，計６ヶの長方形となります．
同様の対応で，29×11の長方形では，対角線が通過する長方形の個数は
29+11-1=39ヶ・・・答 となります．
※「29と11が互いの素」であることが決定条件です．互いに素でない2数の場合は，対角線が途中で格子点を通過しますので，格子点を通らない図形ごと区切ってカウントを加えます．
＜補足＞
■ 私ごとですが学生時代にスルーしてしまいずっと気になっていたガロア理論の学び直しをスタートしました．生涯学習よろしく牛歩の日々を送っていますが，1対応1 が各要所で顔を出します．やはり，1対1対応のideaは根源的であり，未来に繋がる思考だと思いますね．間隔＝植木本数-1 を安直に棒暗記させるような展開は厳に戒めなければなりません．
■ 次回テーマは「1/√2=√2/2 に注目」（予定）です．
■ にほんブログ村ランキング（数学教育）にかかわってバナー↓のclickをお願いします（宣伝が多く恐縮です）．
選択したblogで↓
■ もう一つ．「ブログみる」の紹介
ブログを見るためのアプリです．
世は正に情報過多の時代．しかし1日は24時間しかありません．できるだけ良質のブログと出会いたいものです．
ブログ村が総力を傾注して立ち上げたブログみるに関わっていきましょう．
Your style is unique compared to other folks I have read
stuff from. Thanks for posting when you have the opportunity, Guess I’ll just book mark this blog.
my webpage; 1xbet
Dear 1xbet
I am very happy to receive your kind words.
I look forward to working with you in the future.
※ This has nothing to do with the blog,but today is my birthday（laughs）.
Greetings from California! I’m bored to tears at work so I decided to
browse your blog on my iphone during lunch break. I enjoy the info you
present here and can’t wait to take a look when I get home.
I’m surprised at how quick your blog loaded on my cell phone ..
I’m not even using WIFI, just 3G .. Anyways, very good
blog!
Dear 7 casino reveiew(1xbet)
I am grateful for the connections I have made with people in California through mathematics.
I was a high school mathematics teacher.I have a lot to reflect on,so I started this blog.
Thank you.
I do not even know the way I stopped up here, however I
assumed this submit was once great. I don’t understand who you are however certainly you’re going to a well-known blogger should you are not already.
Cheers!
Dear บาคาร่า68(misocon)
Thank you for your kind comments. I started this blog as a reflection of my time as a teacher and a feeling of unfinished business. I want to use everyday objects as teaching materials for mathematics. By the way,Do you know Japanese origami? I’d like to introduce you to an origami blog. See you next time
https://math-negi.jp/2020/07/07/origami-and-math/
Hi great blog! Does running a blog like this require a large
amount of work? I have virtually no expertise in coding but
I had been hoping to start my own blog in the near future.
Anyway, should you have any ideas or techniques for new blog owners please share.
I understand this is off subject but I simply wanted to ask.
Thanks!
Dear ดูขอนไพ่บาคาร่า
I’m happy to meet someone who shares the same interests.
I was a high school math teacher. Looking back, there are many things I regret. “I should have made the students think more,” “I taught too fast,” etc. With this in mind, I started a blog.
There is also a by-product. By starting the blog, I have been able to look at math throughout the entire 12 years of elementary, middle, and high school. This is a very valuable asset.
Thank you for your positive comments.
* Here is a blog with a video (image of the overlapping part of two cylinders)
https://math-negi.jp/2020/09/03/three-dimensional-feeling2/