1/1.414 ≓ 1.414/2 ← どこか引っ掛かる…
有理化の代表例 \[ \frac{1}{\sqrt{2}}=\frac{{1}・\sqrt{2}}{\sqrt{2}・\sqrt{2}}=\frac{\sqrt{2}}{2}…… A \] ということで話はスムーズに進んでいきます. ただ,A から \[ \frac{1}{1.414}≓\frac{1.414}{2} \] とするといかがですか?ホントに左辺右辺は一致する?!
分母の有理化は確かに「そのとおり」

■ Aにおける式変形は見事に「そのとおり」という展開で,子どもたちもナットクせざるを得ないかと.
ただ,根号を使わず小数(近似値)で有理化の式変形を表すとどうでしょう.
有理化を小数で示す
■ √2≓1.414 で近似して改めてAをじっくり観察します.
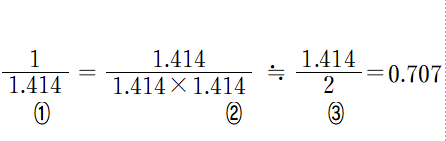

■ ③はラク過ぎて省略しますが,同値である①との負担・作業量にはエライ違いがあります
⇒ 実際に①③を計算させて「負担差を体感」してもらうことがpoint
⇒ この時間負担を惜しんではならないと考えます.後々,種々の定理や公式を学ぶ際の姿勢に直結します!
定理・公式によって思考が楽になり,時間短縮につながる
子どもたちは数学リーダー(指導者)の”先を見通す力“の有無を見抜きます(園児だって分かる子は分かります).
計算量の違いはどこから?
■ √2 とは,平方すると2になる(正の)数・・・※1
だから,√2²=2 これ以上の説明は不要!しかし,ちょっと待ってください.
1.414×1.414≓2 ・・・※2 としたとき
「※1と※2が同じことを主張している」と理解していないヒトがいます(必ずいます).
√2: ヒトヨヒトヨ…,√3: ヒトナミニ… と暗記させても実態が”棒暗記”になっている場合ですね.
■ 上式②をジックリ観察します.
たとえば \[ \frac{1}{5}=\frac{1×5}{5×5} \] と左辺→右辺へ複雑に変形することはまずありません(分母が分数や小数の場合を除いて). ところが \[ \frac{1}{1.414}=\frac{1×1.414}{1.414×1.414}≓\frac{1.414}{2} \]このように,分母の有理化においては,分数をあえて複雑にしています.
でも結果としてこの変形が合理的であるワケは
ひたすら 1.414×1.414≓2 ・・・ ※3 という事実に基づきます.
⇨ 折にふれて、筆算で左辺を計算する・させましょう
平方根や三角関数,対数表etc の作成者に敬意

■ √2,√3,√5 …についての近似値は昔から求められていました.そろばんや電卓,ましてPCもない時代でしたが,関係者たちが分担しながらアナログ作業したことと推察します.
※ 試しに開平法で√2を求めてみてください(かなりメンドーです).
■ ヒトは,√2や√3のように新たな記号や関数記号で新たな数を編み出してきました.
例:三角関数:sin1°≓0.0175,常用対数:log2≓0.3010,指数関数:10^(0.3010)≓2 等々
⇒ 仮定の話。かつて某国に住むxさんが√2, √3等々の近似値を求めたとします.印刷技術の発展もあり、やがて平方根一覧表が作られ,その表は必要とする関係者に伝えられたことでしょう.そしてどこかのyさんは何の苦労なく√3 の値を入手し活用していきます.
⇒ この時間の節約は地球規模で可能となり、科学技術の発展に直結しました。

■ ネイピア(17c, スコットランド)が発案した対数は「天文学者の寿命を延ばした」と言われています.
当時は,大航海時代で航海士たちは天文観測の結果に頼っていました.天文学はとてつもない巨大数を使います.計算機もない時代でしたので天文学者の寿命は短いという話も事実だったのでしょう.
その状況を劇的に変えたのが y=logx 対数関数 だったのです.
※対数関数は,かけ算を足し算にするideaですので,省力化貢献度は極めて大きいですね。
<補足>
■ 次回テーマは「その記号,似ていますがベツモノ!」(予定)です.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介
ブログ村制作のblogを見るためのアプリです.
世は正に情報過多の時代.しかし1日は24時間しかありません.できるだけ良質のブログと出会いたいものです.
ブログ村が総力を傾注して立ち上げたブログみるに関わっていきましょう.