似ている記号の罪:{-, -}{+, +}
すぐれた記号の発案により計算力・思考力はアップします.その反面,似通った記号が独走して「分かったような気にさせる」罪な場面もあります.

中1年が正負の四則計算をよく理解できるな~
■ イヤミではなく,心底そう思います.習う側・教える側,共に大変です.
① 正の数・負の数をひく ⇒ 符号を変えた数を足せばよい
② 異符号の2数の和 ⇒ 符号は絶対値の大きい方の符号,絶対値は2数の絶対値の大きい方から小さい方をひいた差
(③以下略)
こんなルールをたくさん前にしてよくぞ・・・.
中1生の中には数多くのルールを習った結果,算数レベルの 25-12+5 などが計算できなくなったという「同情」例も聞きます.
しかし,多くの子どもたちは,ドリル学習を中心に四則計算を乗り越え高校に進んでいるようです.
でも,記号の「まやかし」は気になる
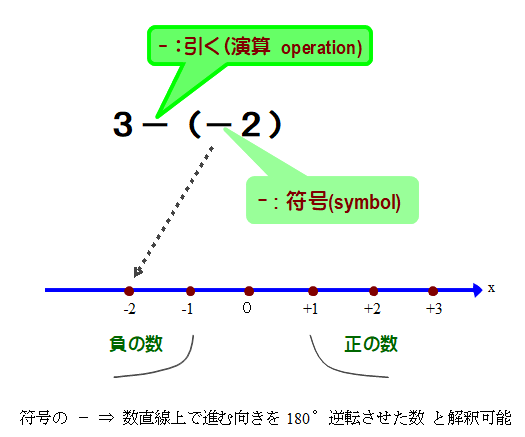
■ 操作(加える・引く)と正・負の符号はそれぞれ同一の記号:+- で示される
⇒ 結果を先に言えば,この両者を区別してもしなくてもナントナク答は求まります
⇒ 問の答が求まることが最低条件だから,多少あいまいさや飛躍があったとしても仕方ない.面倒な理屈にはまって結局,受験問題解けなかったら責任を問われる
⇒ 分かります.しかし,その中でも「あいまいさや飛躍」の自覚ないママ,ドリル学習に突っ込んでいる光景も結構ありそうです
質問・疑問に応える準備
■ 現行教科書の解説はすばらしいと感じますが,ここでは紛らわしい記号をあえて区別して論理を進め,どこかの段階で記号は同一視しても GO となることを確認します.
⇒ 「良心の痛み」のささやかな緩和
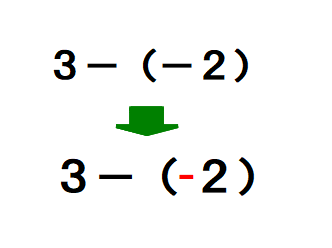
■ 図のように
加える,引く⇒ +と-(そのまま)
正負の符号 ⇒ + と – (赤字で小)
と区別します.
<目標> S= 12-8-(-15)※
をルールに基づいて計算できる(質問・疑問にも答えられるようにする).

■ S=12ー8ー(ー15) を計算するのに,上記のように,原型まで戻って行うべしと主張するのではありません.記号のルールを一つ一つ当てはめて計算すると,S=12+(-8)+15=19 とラクに変形できることを体感したい・させたいものです.※<補足>参照
■ 上記ルール④以外はすべて教科書からの引用です.①③の説明は「秀逸」で.ややもすれば「天下り」解説に陥りやすい箇所への表現工夫に頭が下がります.
④は,ベクトル的な解説になります.-(マイナス符号)に逆向き・反転というニュアンスを持たせたものです.また,-(-15)=-1×(-15)=+15 という解説があったとすれば,それは邪道.
<補足>
■ 本日のテーマは代数学でいう整数環に関することであり,整数の四則演算はいくつかのルール(引き算や負数の約束など)で確立しています.しかし,その内容を解説すれば「演繹」的な構成にならざるを得ず,中1生にはムリ.数学教育初歩の原則はその展開が「帰納」的であることです.
■ 次回テーマは「似ている記号の罪(2弾)」(予定)で,積分記号についてです.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介
ブログ村制作のblogを見るためのアプリです.世は正に情報過多の時代.しかし1日は24時間しかありません.
できるだけ良質のブログと出会いたいものです.ブログ村が総力を傾注して立ち上げた
に関わっていきましょう.


