∫ 積分記号のルーツ
高校数学では不定積分を学んで定積分へ進みますが,どこかおかしくないですか? また,微分記号の( )’ はともかく,積分記号の∫ って,唐突でイキナリですよね.

⇒ 例えば,”健康”の意味を説明する際,”不健康“から話を進めるという手順はふつうはとりません.とったとしても最後に「不健康でないことを健康と言います」と解説を付け加える必要があります.
■ しかし,現行の積分(数Ⅱ)はその「不」からスタートしています.そして「不」不定積分=定積分 となることを念頭に置いて
①逆微分演算として不定積分の導入・・・突然の∫記号の登場!
②その延長としての定積分・・・天下り式!
③定積分の値が面積を表すことの解説・・・かなり”苦しい”!
という展開になっています.
■ この構成全体が「完成品を上から下に流していく」イメージで,教室で積分を創り上げていくシーンがほとんど採れない感じがします.
積分のideaは紀元前から
■ 微積分と一括りしますが歴史はベツベツで,積分(面積計算)がはるかにセンパイです.微分は17c頃の誕生ですが,積分は紀元前3c頃まで遡り,アルキメデスは正96角形を描いて円の面積と円周率の値をほぼほぼに求めております.
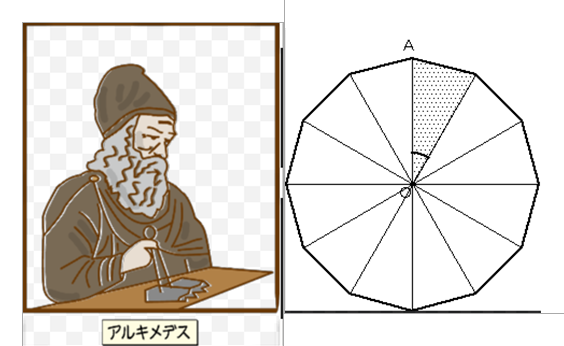
■ 曲線で囲まれた部分の面積を,三角形や長方形にパーツ分割し,それらを寄せ集めれば面積が求まるだろう,というideaです.
この発想を区分求積法といいます.柱状(長方形)による分割が多いですね.教科書(数Ⅲ)の一部を紹介します.
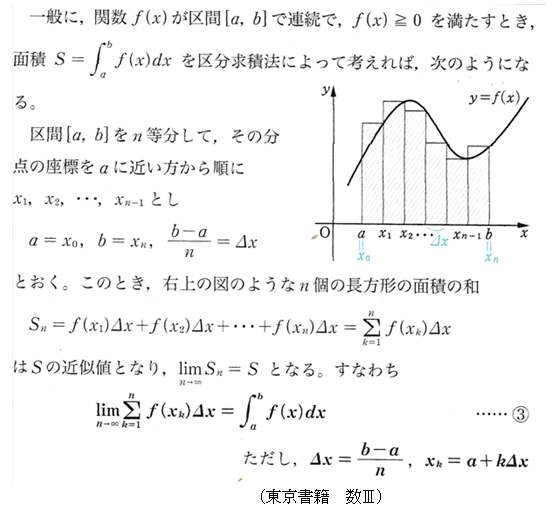
■ 上式から積分記号 ∫ とdx の誕生由来が見て取れます.
・インテグラル∫は伸びたSが元で,そのSは,ギリシア文字Σが大元です.
・dxの大元は増分Δxです.Δxはxが「限りなく0に近いがほんの少し増加する量」というイメージで,グラフでは柱の幅を示します.
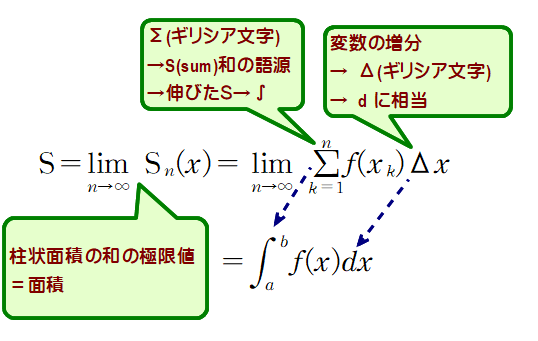
■ 以上のことから,積分は数学史に基づき区分求積法をベースにして構成されるべきと考えます.
数Ⅲの先取りであり時間的制限があることは承知の上です.本格的展開でなくともアウトラインの解説だけでもよいのでは?.
⇒ この場合,定積分の導入は当初から「面積を表す式」となり,逆微分(=不定積分)のカオはしばらく見えませんが後に出ます.そこが「ヤマ」で微積分の基本定理の登場となります.
以下,区分求積法を基にした積分展開した場合の話題です.
積分と微分はベツベツの歩み
■ 区分求積法による求積(面積・体積を求める)では,微分はどこにも登場していないことに注意しましょう.
⇒ 積分と微分がベツベツにあって,微積分 と一括りはできません.
Σ 計算はタイヘン ⇒ 救世主:逆微分
■ 区分求積法で面積計算するとかなりハードで時間がかかりすぎます.
例 放物線 y=x² , x軸, 直線 x=1 で囲む部分の面積Sを求めましょう.
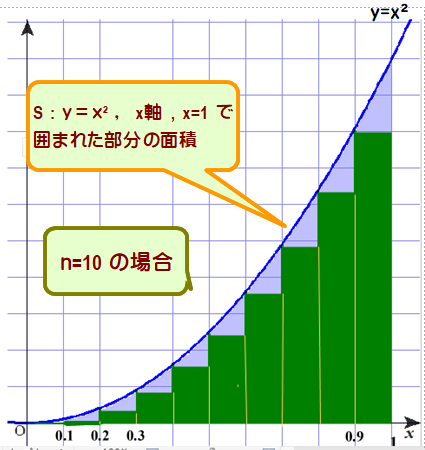
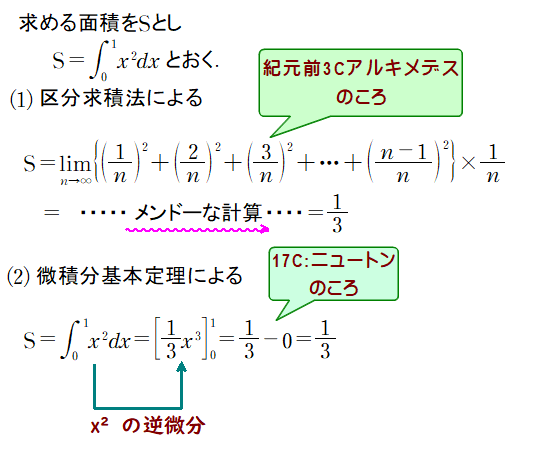
■ 上式で(1)を(2)比べると,(2)のスマートさには驚きますね.(1)(2)間には約2千年の時が過ぎていることにも注意しましょう.
積分計算のスマートさは何に基づく?
■ 積分計算の核心部分を再掲します.

■ 面積計算は,与えられた関数の原始関数を求めることで一気に進展しました.
⇒ 原始関数を求める=逆微分
⇒ ここで初めて積分(≓面積を求める)と微分(≓接線の傾きを求める)が同じステージに上がったワケです.
⇒ 面積が接線(の傾き)とカンケーある!
これは,すごいことではありませんか.この根拠となるのが
微積分の基本定理
です.本定理については,かつてある数学者曰く
小~高までの算数・数学で最も重要な定理である
何が問題なのか?
■ 最重要定理とも称される微積分の基本定理についてですが,高校生の多くは無意識使用であり,興味関心はもたないようです
⇒ 意味理解なしの機械的反復練習へ一直線?
■ 背景の一つに,2つの積分記号(不定積分と定積分)に共通の∫ 記号が含まれていることがあると見ています.
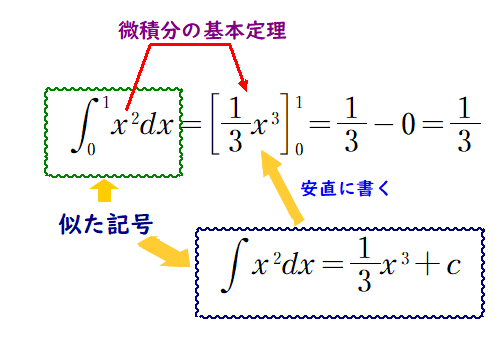
⇒ 上図で,微積分の基本定理の意味と意義をしっかりと押さえ,微積分全体を俯瞰する,これが取るべき本来のスタンスです
しかし,少なからずのヒトは,似た記号∫が用いられていることをコレ幸いにと,機械的な積分(逆微分)計算に走っています.
■ 数Ⅱでは区分求積法は扱いません(→数Ⅲで).このこともあって現行の教科書に準拠すると論理展開に困難があり,ムリヤリ・不自然・飛躍 の解説がなされる面も理解できます.
しかし,似た記号があるからと言って「計算タダ乗り」はいただけません.
<補足>
■ 微積分の基本定理について,教科書では内容は当然解説していますが,基本定理と銘打っていないケースが多いです.理由は不明…
■ ∫記号を巡るゴタゴタは,時間数配分だけに原因があるのではありません.微積分全体が完成した後,数学を十分理解したヒト(≒数学者)が,天下り式に記号を当てはめたことに端を発していると考えます.つまり,似た記号を使用すれば,シモジモの民の記憶再生に役立つだろうと(邪推か).
■ 次回テーマは「まちがい常識」(予定)です.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介
ブログ村制作のblogを見るためのアプリです.世は正に情報過多の時代.しかし1日は24時間しかありません.できるだけ良質のブログと出会いたいものです.ブログ村が総力を傾注して立ち上げた
に関わっていきましょう.