asinθ+bcosθ:合成 ⇒ 唐突感のカイゼン
y=3sinθ+2cosθ という関数は,y=√13sin(θ+α) と変形(合成)できます.この合成公式,唐突に√13 や 意味が分からないα が登場しますので,評判よろしくない公式の代表格です.
突然,√a²+b² でくくる ⇒ これが不評
■ 唐突感ある授業の場合,その多くは,一方通行で,天下り式の展開となります.
■ √13や α が登場する舞台裏,また,そもそも合成自体の必然性の理解も得たいですね.

すばらしい質問
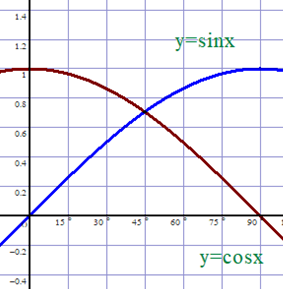
Q 「y=sinθ と y=cosθ は性格が反対.第1象限では,前者は単調増加,後者は単調減少.すると,y=sinθ+cosθ という関数は,互いに打ち消し合って,フラット,つまり,x軸に平行な直線になる,あるいはそれに近い曲線になるのではないか?」
何ともユニーク,かつ,一考に値する見方です.このような発言(つぶやき含む)や疑問は”大歓迎”ですね.内心「よくぞ言ってくれた」という思いを抱きます.
■ 例:y₁=x, y₂=ーx+2 なら,y₁+y₂=2 となり,確かに一定値2 となりますね.こんなイメージでしょうか.
予想して式化を試みる
■ そこで,y=f(x)=sinx+cosx で,xが適当な角のときのyの値をマークしてみましょう.グラフ作成には,本blogでしばしば登場する画像フリーソフトgrapesを使用しました.
下図で,点Pのy座標●+点Qのy座標●=点Sのy座標● です.
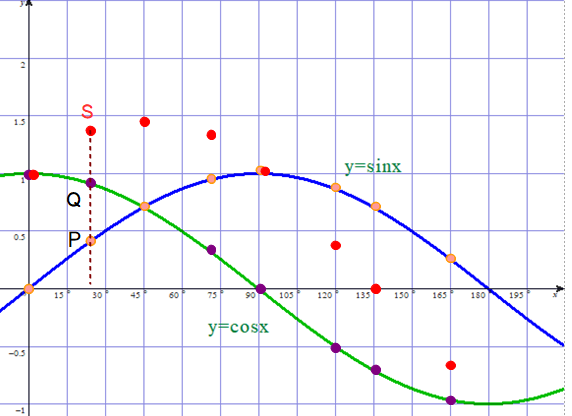
■ 上図で,●の軌跡を眺めると,フラットな直線にはならず,なめらかな曲線,しかも,周期性もありそうですね.次の図を見てください.
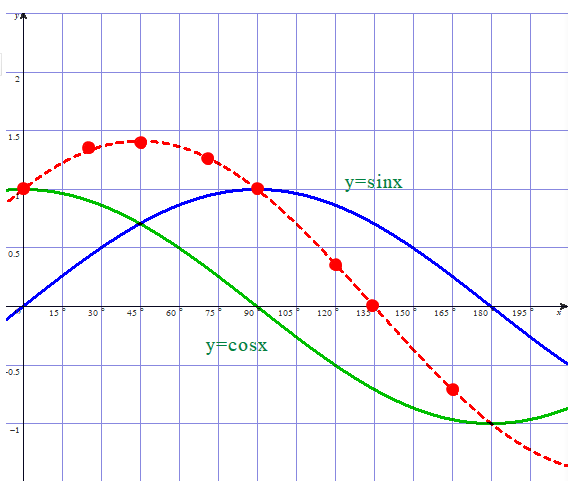
■ 上図で,曲線(赤点線)の式を求めてみましょう.
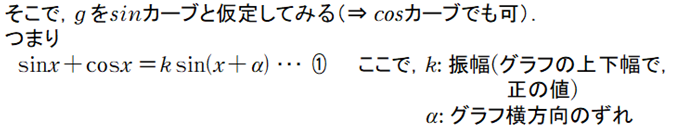

■ 仮定がpointですね.
もし,f(x)=5sinx+2cosx のときはどうなりますか.
②,③ ⇒ 5=kcosx ・・・②’ 2=ksinx ・・・ ③’ となり,それぞれ平方
⇒ 25=k²cos²x , 4=k²sin²x
⇒ 辺々加えて,25+4=k²(cos²x+sin²x)=k² ∴ k=√29 となります.
したがって,f(x)=asinx+bcosx のときは,k=√a²+b² が登場するワケです.
唐突感とどう付き合う
■ 数学は「体系的な学問」ですので,学びの途上で,”天下り”の解説を避けることはできず,そのつど”唐突感”が発生するものと覚悟しなければなりません.
■ 算数数学のリーダーは,”天下り”箇所に入ると,①子どもの多くは,「キョトン」とするだろうという覚悟を持つ ②何らかの緩和策を講ずる(背景・舞台裏説明に努めるなど) の2点を踏まえた対応を心準備しておきたいもの.
一番困るケースは,”天下り”の解説をしているという自覚を欠いている場合ですね.⇒ 無自覚の指導は罪深い!
<補足>
■ 次回は,「共通テスト 数ⅠA”山の仰角”あれこれ」(予定)です.過日,第2回大学共通テストが実施されましたが,全体的に難易度が上がったというほか,話題になった数学の問があります.数学の問題がマスコミに取りあげられるのはほとんどありません.
■ 「にほんブログ村」のバナーをそれぞれClickしていただければ幸いです.(最初:左, 次:右)