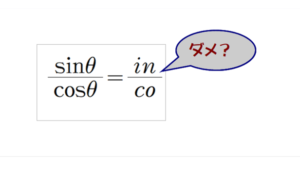感染率拡大緩和 ⇒ どのカーブ?
■ 今日的な学力として資料の活用が注目されています(昔風に言えば,統計処理の初歩). 現下のコロナ関係でも,感染数値のタイトルが日々発信されています.
■ ”感染者数 高止まり”,”感染率拡大緩和” etc ・・・どんな意味でしょうか.”土地公示価格,県内下落幅,0.6%縮小” はいかがですか.ヒトにより微妙な解釈の違いもありそうです.実は,”意味理解”は,微分と直結します.
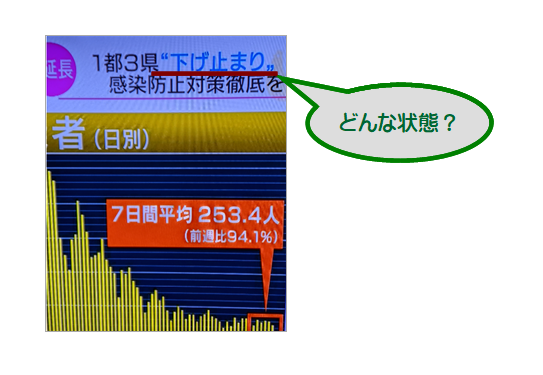
■ そこで,理解・解釈を深めるため,ナント「微分」まで持ち出してみました.
記事と合うグラフはどれ
A

B

C

①
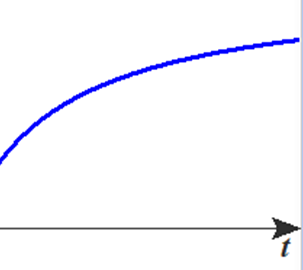
②
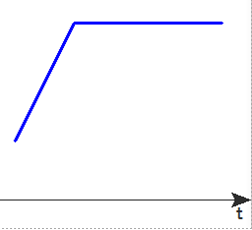
③
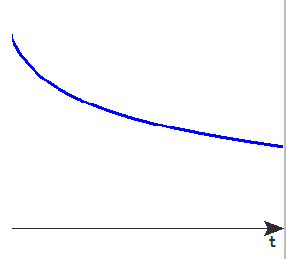
④
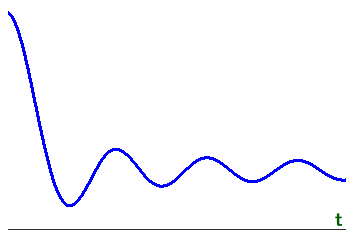
<正解> A- ③ B-① C-③ or ④
■ Cについては,疑問・異論もあるかも知れません.
■ ②の直線についてです.なぜ「はじかれた」のでしょうか.
直線的変化は少数派!
■ 「直線的変化≓比例」です.小学校以来,変化と言えば,比例,すなわち直線をイメージするようにしつけられてきています.しかし,これまで紹介した数例からも分かるように「世の中の変化」は,比例で示されるように単純ではないことがわかります.
2倍努力すれば,テスト点数が2倍になるとは限らないからです.
■ 「緩和」「下げ止まり傾向」これらは,”徐々に変わる”という変化を基にした言い方ですね.
これらは関数で言えば,1次関数ではなく,指数関数に近いのです.そして,指数関数と三角関数は親密な間柄ということも押さえておきましょう.
変化を微視的に見る ⇒ 微分への道
■ これまで述べたことは,直線を,つまり比例関係を軽視したのではありません.
むしろ逆です.比例関係を最重要視するがゆえに見方を変えただけです.

■ 例:感染拡大 緩和
感染者数をy,横軸を時間tとします.
①感染拡大 ⇒ yは増加関数 ∴ y’>0
②緩和 ⇒ yは「伸び悩み」
つまり
③yの増加率が減 ⇒ (y’)’=y”<0
■ したがって,「感染拡大 緩和」の様子をグラフで示すと次のようになります.
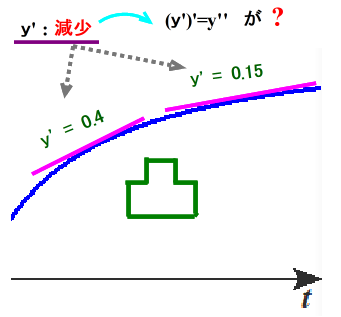
■ 今回は「記事見出しと微分」でしたが,日常生活の中に数理が潜んでいることにもっと鋭敏なセンスを持ちたいもの.
■ 教科書での学びと,生活数理を結び付けること,それは大人の責任です.
■ 微分係数y’とは,曲線上のある点における接線の傾き(=tanθ)を示します.
→ 詳しくは”平均の速さの行き先”で解説
つまり,曲線を細かく見ると,直線の集まりからなっている!⇒ 微分のidea
グラフの例では,y’=0.4 , y’=0.15 ですので,接線の傾き具合が減少している⇒ 曲線の変化がなだらか(緩和)⇒ y”<0
■ 以上の様子を式でまとめて表すと
感染拡大緩和 ⇔ y’>0かつy’’<0
ある区間で y’’<0 のとき,グラフはお椀を伏せたような形状になることから
上に凸
といいます.
例 y= -x2 → y’= -2x → y”= -2<0
y= -x2 のグラフは上に凸の典型例ですね.
<補足>
■ 次回テーマは「文字でつまずく」です(予定).何十年もこの「文字」が克服されていません.ここでは改善策を講ずる前段階として,文字でオロオロする子供の心理を探ってみます.ここが分かんないと「策」も立てられないはず.
■ 「にほんブログ村」のバナーをclickしていだだければ幸いです(はじめに左, 次に右).