たかが”植木算”

よく知られている植木算についてです．ある距離に一定間隔で木を植えたときの，木の本数，間隔数，そして距離との関係を，ちょっと”引っ掛け”も細工したりして問う問題です．

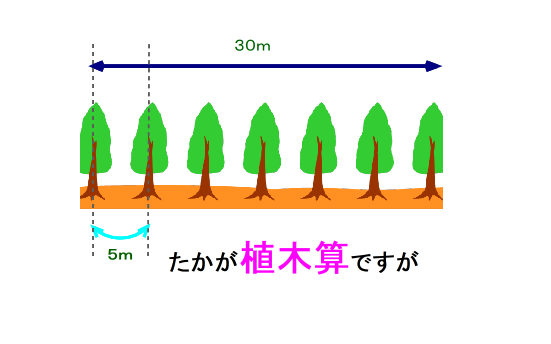
■ 上の図の場合は両端にも木を植えることより，５m×６本＝３０m となり，

　　　（木の本数）＝（間隔の数）＋１

となるわけです．これを基に，次のような内容が公式（or まとめ）として紹介されています．

よく目にする植木算公式です･･･

■ Ⅰ 両端に木を植える　：木の本数＝間隔数＋１

■ Ⅱ 両端に木を植えない：木の本数＝間隔数－１

■ Ⅲ 循環して木を植える：木の本数＝間隔数

⇒ 納得しやすい公式で，問題への対処もスムーズにいくかと．ただ，次のような問に対してはどうでしょうか．

”暗記” タイプではない植木算

■ 公式には大別して２タイプ．

①暗記タイプ（←思考・時間の節約のため）･･･三平方の定理，２次方程式解の公式，余弦定理など　

②プロセス重視タイプ･･･比例公式(a/b=a’/b’)，植木算公式など　

どちらのタイプも，活用しつつ次第に身に付けていくことが肝要ですね．

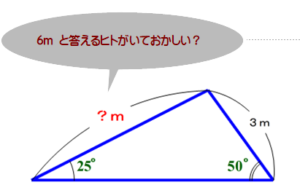
■ 上のＱ です．植木算ということで上記公式Ⅰ～Ⅲを適用しようとするわけですが，結構手こずるヒトが多いのでは．苦し紛れに，(1000-100)÷7 などと計算を始める方いませんか？

植木算は，プロセスに本質あり

■ 植木算公式「Ⅰ：木の本数＝間隔数＋１」を導く際，よく目にする解説です．

「30mの距離を5mずつ区切ると，間は6つできますね．このとき，木は7本でしょ．このように･･･」

率直に言います．この解説には，奥行きも深さもなく，したがって，次に活かせる発展性も”なし”です．

■ 3以上の数詞を知らない未開地でも，ヒトビトは互いに食物を平等に分けあってきました（多分）．5 も 38 も知らない（カウントできない）のに．なぜ？ 植木算にそのヒントがあります．

植木算 ⇒ カウント×，対応〇

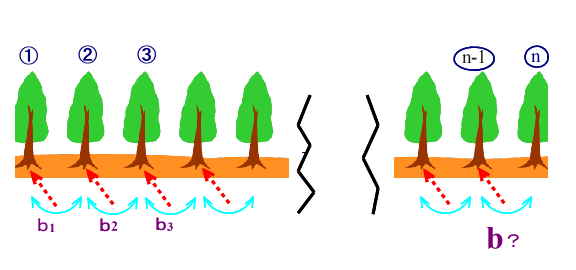
■ 上の図は，「一番左の木① ⇔ 一番左の”間”ｂ1 」を対応させている様子です．

以下，同じような操作により，②⇔ｂ2 , ③⇔ｂ3 とします．

■ すると，最後の”間”は，ｂの何？

当然，ｂn-1  となります．

その際，改めてｂ1ｂ2ｂ3･･･と，順に数え上げること（カウント）は不要で，対応した木の”割り当て番号n-1″をそのママ使用すればよいわけです．

 

■ ２つの集合があり，それぞれの要素a,bを何らかのルールで対応させること

　　　　a → b 

は，関数の原型（本家）となります．

※ なお，数学では，似たような意味で”写像”という概念もあります．対応とほぼ同一です．また，対応の中でもっとも有名なのが，１対１対応（one to one）です．

 

次は，よく知られている問題です．

Ｑ２ 格子状の道路があります．点ＰからＱへの最短コースの取り方は何通りありますか．

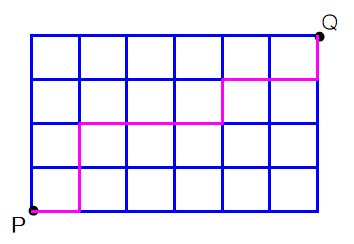
Ａ２ 解き方の一例．

最短コース ⇒ つねに，右1つ(R) か 上１つ(U) のルートをとる

これ以外のルート（左や下）をとると，その瞬間，アウトになりますね．

図の例：RUURRRURRU と示されます．このように，

最短コース  ⇔  R:6個，U:4個 を一列に並べた順列　

          （１対１対応）

したがって，同じものを６つと４つ含む順列の総数ということで，

　１０！÷（６！×４！）＝２１０（通り）

ところで，このQ２ですが，各格子間距離が一定でない場合はどうなりますか？

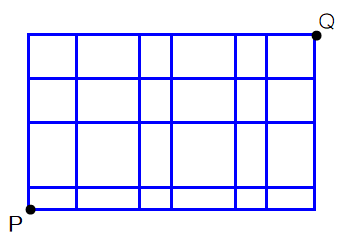
改めて，数列とは何でしょう？

■ 数列｛aｉ｝は，ｉ→ ａi （i=1,2,3,･･･）という対応です．

したがって，a1 ~ aｎまでの個数を調べるときは，カウントしなくてもよいのですね．ｎ自体がその個数を示しているからです．←カウントしたとすれば，二重作業をしたことになります．

冒頭で取りあげたQの数列による解答例は次のようになります．

※ 末項の998が求めづらい（求めたくない）ときは

　　　７n+95<1000 ∴　n<129.2

　この不等式を満たす最大整数nは，n=129･･･（答）

■ 数列を使用しない解答例

102 と 998 を探し求めます．

998-102=896 ,　896÷7=128

つまり，間隔数：128 なので，求める解は，129個

階差数列のツボ

■ 数列は，①等差数列　②等比数列　③その他（雑）数列　と大別され，実際，この順に習います．

■ 「雑」数列を前にすると，平方数列や逆数列など(例：1,4,9,16,25,･･･),見た目で直ぐ形が理解しやすいを除き，ある項とその前の項との差をとって見たくなりますね．この差からなる数列を（第一）階差数列といいます．

　例　　　　3 , 8 , 15 , 24 , 35 ,･･･　

　階差数列　  5,　7,    9,   11, ･･･

ここで，階差数列が式化できるときは，元数列も式化できます．この階差数列と植木算がバッチリ繋がっています．

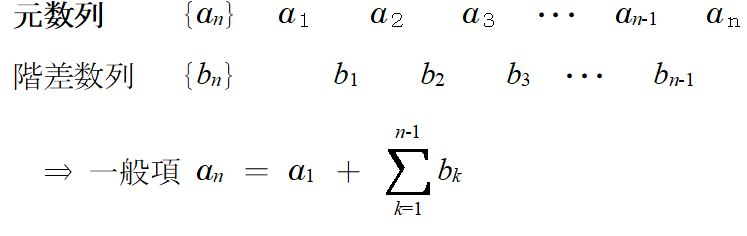
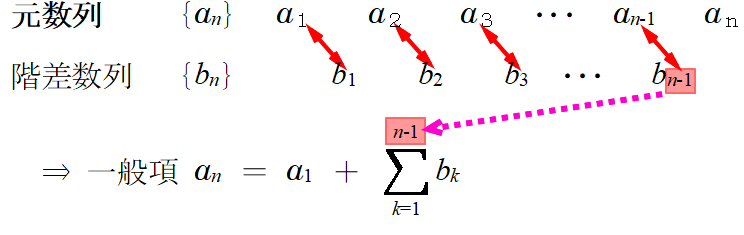
■ 階差数列の末項bn-1 （＝Σ記号の端数）がスムーズに出てこないヒトもいます．「対応」が見えれば，カウントは不要です．

■ 次回テーマは，「必要感をもたせる」（予定）です．今日，新課題が次から次へと学校教育に押し寄せています．加えて「コロナ」です．時間不足ですね．が，そういう状況下であるならばより一層，学ぶ意欲喚起に繋がる”必要性”に目を向けましょう．

■ 「にほんブログ村」のバナーをclickしていだだければ幸いです（はじめに左, 次に右）．