数の大元は “大小判断”
数の感じを数えることと混同してはなりません(ダンツィク「科学の言葉=数」岩波).音の発声が直ちに会話にはならないと同様,数の感じから数える(数の誕生)までは,気の遠くなるような時間がかかりました.
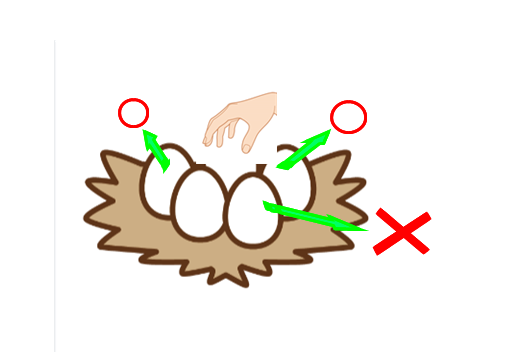
■ 数の感じとは何でしょう.ダンツィクは,ある鳥の例を紹介しています.
鳥が巣から離れたとき,巣にある卵を一つずつ抜き取っていく.その鳥は,残り3個まではソノママでいるが,残り2個なると,異変に気付いてその巣を捨てる.
⇒ その鳥は,4と3の区別は付かないが,3と2の違いは認識できると考えられる.
■ 「3と4の区別が付かない」の言い方ですが,この表現は誤解を与えるかも知れません.
鳥はもちろん,太古の時代のヒトは,数詞の3や4を知らないからです.
⇒ 正しくは「鳥は,今日,私たちが使用している数3や4に相当する量の区別ができない」となりましょうか.
■ バートランド・ラッセルは次のように述べています(blog”9の次は10” 再掲).

”ペアのキジ(鳥)”と”両日”は,いずれも2という数の実例であることを人類が発見するには多くの時代を要したに違いない
確かに,2という数が道端に落ちているわけではありません.数はヒトの創造です.
■ 数の感じ程度(2と3の違いが認識できる水準)から,ラッセルが述べる数獲得までのプロセスを知りたいところですが,正直申して当方の手に負えないテーマです.想像は出来ても,実証的に示すリキがありません・・・.
■ ただ,数の感じ の実際は,間違いなく,コレです.
まずは,大小判断

■ ヒトビトが土器や狩の道具などを製作し始めた頃を想定します.
ようやく手に入れたであろう食料を,どのような方法で分配しあったのでしょうか.
■ まず,肉の塊や木の実を前にして,見た目や重さの感覚で大きさの違いを認識します.そこで,大きさを整えたり,個数の増減をします.
■ すなわち,数の感じの活かし方の第一歩は,大小の判断であり,「数」の出発点になります.
ただ大小判断は1回では済みません.なぜなら,ヒトはグループで生きていたからです.
他のメンバーも納得するような分配手法を日々取り続けなければなりません.
⇒ 大小判断をより多く,より詳しくします.この流れが必然的に「数」の誕生に向かっていきます.

■ 時は過ぎ,ヒトは数を創造し,今日に至りました.今日では,ヒトが誕生して,数年後には「いち,に,さん,・・・」と数え上げ,幼稚園児の頃には100まで数えて,親を喜ばす光景もよく目にします.
人類が数万年もかけて得た能力を,わずか数年で獲得させるシステムには畏れ入ります.
■ ここで注意することがあります.
それは
必ずしも 数詞を唱えることができる=数を理解した ではないことです(唱えることは,ある意味でお経みたいなものですから).
特に,学ぶ過程で,数量感が伴わないレッスンを受け続けた場合は,遅かれ早かれ壁にぶち当たります.
■ この視点で,21世紀になった今日でも,ときおり,数や量の大小を確認することは,原点回帰という視点から意義深いことです.
大小判断の根拠
■ 次の各問で,数や式の大小を調べなさい.
Q1 ①5+5+5+5+5+5+5,②7+7+7+7+7,
③1+2+3+4+5+5+5+4+3+2+1
A1 ①=②=③ です.計算して結論を出すべき問ではありません.図で矢印の方向にカウントすればよいですね.数を図と絡ませることは,原点回帰の一つです.

Q2 ① 2.236×2.236 ② 5
A2 ①<② ですが,①を実際に計算してはいけません.
√5=2.236・・・ より,2.236²<5=√5² ∴ ①<②
計算してしまったヒト ⇒ √(根号)の意味がホントは分かっていない!
三角方程式:sinθ=√3/2 でθが即答できない高校生のほとんどは,√3をヒトナミニとは棒暗記していますが,√3/2≓0.87→0.9弱 という認識を持ってないため,y(=sinθ)≓0.9弱の直線が描けません.
Q3 ① 24÷3 ② 24÷0.5 ③ 24÷2/3 ④ 24÷30 ⑤ 24÷0.2 (blog”□÷0.8“再掲)
A3 これも実際に計算したら意味半減(いや,意味全減)です.
④<①<③<②<⑤
※全国学テ調査結果から,正答率は5割程度と見ています.由々しき実態ですね.

Q4 10人の生徒がいます.①3名の委員の選び方 ②委員長1名,副委員長1名,書記1名の計3名の選び方
A4 本問は, 高校数学の順列・組み合わせという領域の内容なのですが,小学生でも十分理解できます.
①と②の大小が分からないママ,次に進むべきではありません.
数学というより,読解力向上という視点から,題意を納得するまで,数学リーダーは腹をくくってトコトン付き合うべきです.個別指導になるかと.実際の計算はその後です!
Q5 ① sin0.1 ② 0.1
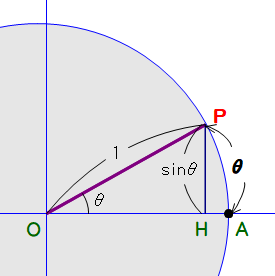
A5 ① < ②
面食らうヒトも結構いるのではと予想します.
図で,∠POA=θ とすると,弧PA=θ , PH=sinθ です.(弧度法と三角比の定義より)
すると,PH<弧PA より,sinθ < θ
θ=0.1 のとき,sin0.1< 0.1 となります.
<補足>
■ 計算力はとても重要ですが,計算自体の意味理解が伴わないと,いつか壁に当たります.
■ 次回のテーマは,「π=3 はダメか?」(予定)です.かつて物議を醸した例の話ですが・・・.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


