責(攻)められる三角関数!
過日,ある国会議員が財務金融委員会で「三角関数より金融教育を」と発言しチョット話題を呼んでいます.※かつて,鹿児島や大阪の(元)知事も三角関数を例に挙げ持論を展開しております.
三角関数は責められる易い?
■ 議員は,数学全般を踏まえた上で,時代が要請する金融教育の重要性を説き,その対極に三角関数を置いたのです.2次関数やベクトル,微積分ではありません.
なぜ三角関数でしょうか?
思い当たる節
■ 金融教育の「引き立て役」として,つまり,悪役の代表に三角関数を挙げたワケです.
思い当たる節があります.次は,埼玉県高校数学標準テスト(2013)の問とその結果です.
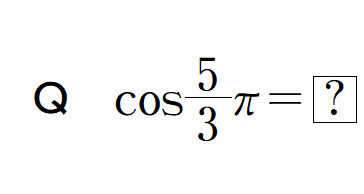
■ 正答率は41%でした.同テストは年度末2月実施で,履修直後や受験生対象ということでもなく,かなり実態を反映した結果かと.
弧度表記でなく,60分法による問(=cos300°) であれば,正答率は数%は上がるかも知れませんが,よくて50%くらいでしょう.経験からして妥当な結果と思います.

⇒ 上記Qは三角関数という領域の中で,その関数値自体の問です.基の基,つまり,三角関数の入り口相当における理解度がせいぜい半分程度という実態!
⇒ 小中高の算数数学を通して,入り口段階でこんなにわかってない領域は他には見当たりません.
⇒ あげくに,cos150°=-√3/2 など,有名角の関数値の暗記まで強いられる現状も散見され,生徒も含めた国民から恨みを買っても仕方ありませんね.
三角関数=悪役 からの脱却
■ まず数学リーダーの指導展開についてですが,失礼ながら創意工夫の不足感を抱きます.
ここでは具体に
①三角関数の公式が多いこともあって,暗記作業にかなりの重点を置いている
②「三角関数の未来」を語っていない
の2点を挙げます.
■ 三角比を含む三角関数が測量分野で利用されている例は教科書にも掲載され,ナルホド感は持てましょう.
しかし,そのレベルだけで終わり,その後は,問題解きが延々と続き,”公式の適用例理解と暗記”というイメージが強いようです.結果・・・国会でやり玉に挙げられる! 無情!²
「この商品を買った人はこんな商品も買っています」舞台裏
■ 次に”三角関数の未来”についてです.何言っているか不明でしょう.ここで週刊「ダイヤモンド」(‘18.6.30)特集号を紹介します.
ネットで何か購入すると,即「この商品を買った人はこんな商品も買っています」というオススメが次々と届きますね.どんな仕組みがあるのでしょう?
■ 実は,舞台裏で三角関数が決定的な役割を演じています(この箇所,当blog“内積って何だ?“の一部再掲です).



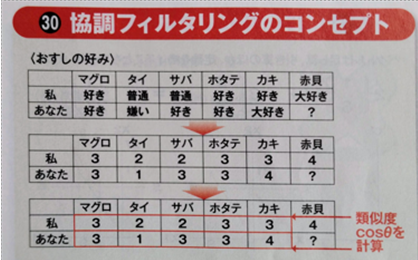

■ このようにして各商品との類似度を計算します.
⇒ 大切なことは,あらかじめ「近いモノ」を絞っているのではありません.各商品ベクトルとの内積を瞬時に計算して,cosθ=1(つまり,θ=0) に近いモノから順に紹介するのです.
内積と言えば,受験数学問題で一役を担っていますが,問題解きのためのツールだけで終始している現状がありますよね?
即,使えること=有益か?
■ 「三角関数の学びを通して数学的処理・思考を学ぶ」ということ,つまり,学びを学ぶという意義が本質かと.
■ 教室内文化から言えば,知的好奇心の喚起の格好の例となります.今回は触れませんでしたが,フーリエ解析でほぼほぼの関数すべてがsinθで表される事実など,ビックリしませんか.
⇒ 音や光,振動,医療分野などに応用されていて,スマホの中にはsinθがビッシリと詰まっております.こんな教材をスルーさせたら,モッタイナイ!
以上のことから,金融教育と(少なくとも)三角関数とを対峙させるべきではないと考えます.
<補足>
■ 次回テーマは「だ円に見えない!」(予定)です.立体図形攻略の一助になればと考えました.素朴な教具製作を紹介します.
■ 三角関数値の定着度把握に絡んで,大学入試センター試験問題の各設問正答率を調べようとしましたが不明でした.たぶん非公表です.公開しない理由を知りたいところ.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).

三角関数の教え方に問題があるのでしょうね。そこを何とかしたいと思いながら、なかなかいい方法を思いつかないです。
現代的な視点が必要なのだと思いますが、そういう現代的な視点との接点がなかなか見つからないです。もちろんフ―リエ級数とかフ―リエ変換とかはあります。これを普通のテーラー展開と比較した議論をするとか、いろいろ工夫をすることは必要でしょう。
ヒッポ・ファミリークラブの『フ―リエの冒険』なども参考になるかもしれません。
少なくとも現代の話題につながる視点がほしいと思っています。
aoyama 様
三角比・関数について「同好の士」とお会いできたような気がいたします.
計算力と意味・意義の浸透,この両立を目指しつつも,三角比・関数の計算だけでアップアップの状況と認識しております。そして,中学校までの比例の単純な考えで解いてきた問題も,中途半端に三角比・関数を習うとその問が解けないという皮肉なケースをたくさん見てきました.数学リーダーの責任は大きく,その分,やりがいもあると思うことにしました.ご指摘のように,子どもたちの身近にある世界との接点を意識的に取りあげる工夫…高校工業や物理,中学技術,経済等々との接点探し…が大切でしょうね.
※『フーリエの冒険』は名前だけで中身は不案内です.入手して何とか吸収したいと思います.