「円錐の斜平面cut ⇒ だ円」を体感する
2次曲線(放物線・だ円・双曲線)は,(直)円すいを平面でcutした際,その切り口として現れます.
円すいは3次元,平面は2次元の図形ですから,2次曲線は,3次元と2次元図形の境界で見える曲線ともいえますね.(下図は,東京書籍数学C)
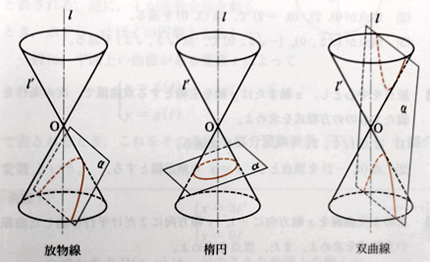
■ 今回は,だ円に注目します.

■ まず,左図のように,円柱を斜平面で切り取ったときの切り口がだ円になることはよろしいですね.中の図は「かぐや姫とだ円」です.右写真はレストランでよく見かける注文伝票を差し入む器ですが,確かに切り口はきれいなだ円をしています.
だ円の証明
■ 直円すいを斜め平面で切ったときの切り口がだ円となる証明は結構大変です.次は「数学とは何か」(岩波)で紹介されている”お見事”な図解による証明です(1822,Dandelinによる).
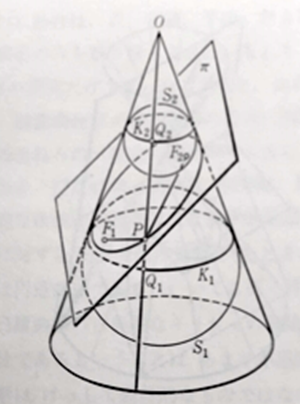
■ <略解> 図で
π: 平面, E: 求める曲線,P: E上の任意の点
S₁,S₂: それぞれ直円すいとπに内接する球
F₁,F₂: それぞれπとS₁,S₂との接点
K₁,K₂: それぞれ直円すいとS₁,S₂と接する円
Q₁,Q₂: それぞれ直線OPとK₁,K₂との交点
とする.
このとき,PF₁とPQ₁は,Pから球S₁への2本の接線であるから,
PF₁=PQ₁ ① ,同様に,PF₂=PQ₂ ②
①+② とすると,
PF₁+PF₂=PQ₁+PQ₂ である.
ここで,右辺は,2円K₁,K₂間の円すいに沿った距離であるので一定値である.
よって,左辺 PF₁+PF₂=(一定値) これは,点Eの集まりがだ円であることを示している.なお,F₁,F₂ はだ円の焦点になる.
やはりだ円に見えない!
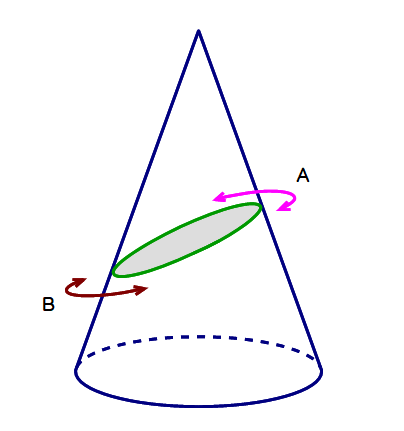
■ 巧みな証明には感服するのみで,理屈・理論は分かりました.が,切断面がどうしてもだ円に見えないのです!(⇒ 少数派 or 私だけ?)
特に,上図でA,B箇所におけるだ円の曲がり具合(曲率)が同じに感じられません.
平面は,A辺りでは母線(右)と直角に近い角度,B辺りでは母線(左)と鋭角で交わっています.つまり,交点付近では円すいの曲がり具合が異なるのに,A,B箇所における曲率が同じになるのが不思議に感じるわけです.
※ 底面に平行な平面と円すいとの切断面は円です.A辺りの円は,B辺りの円と比して小さい円となります.曲線(だ円)が母線右に対してやや膨らみながらカーブしてきてもその付近が小円のため膨らみが減衰される,B辺りの曲率はこの逆になるので,結局,両者は一致するのか?と”情緒的”に理解しています.
それなら円すいで「実感」しよう
■ そこで,この曲線がだ円であることを体感すべく「現物で確認しよう」と努めました.身近に直円すいはなかなかありませんが,近くのDIY店で作業用コーンを見つけました.先端部がないじゃないか!などと責めないでください.


■ 当初,ノコギリで斜め切断を考えましたが,これはムリ!です.斜めに,かつ,その方向に真っ直ぐ切り続けることは,板でも難しく,ましてプラですから.
⇒ 失敗するとコーンを再度購入するというのがつらい!
市販の教具・・・木製が多いのですが小さくて迫力に欠け,また,けっこう値も張ります.
3Dプリンター・・・円すいなど単純な立体製作には適用すべきではありません.
■ そこで,発想を逆にしました.
結果的にだ円となる ⇒ プラ板面にだ円の穴を切り抜く ⇒ それをコーンに被せる ⇒ ピッチリと収まることを確認する
実際の作業

■ コーンの大きさから適当なサイズのだ円を想定して,長軸・短軸の長さを測定します.
今回は,サイズが長軸:20cm, 短軸:12cm のだ円が円すいから切り出されることを確認しました(もちろん,別のサイズでもコーン内であればok).
⇒ 長軸:短軸 = 20:12=5:3
■ 次に,長軸:短軸 = 5:3 の正確なだ円を図形ソフト(grapes) で印刷しました.
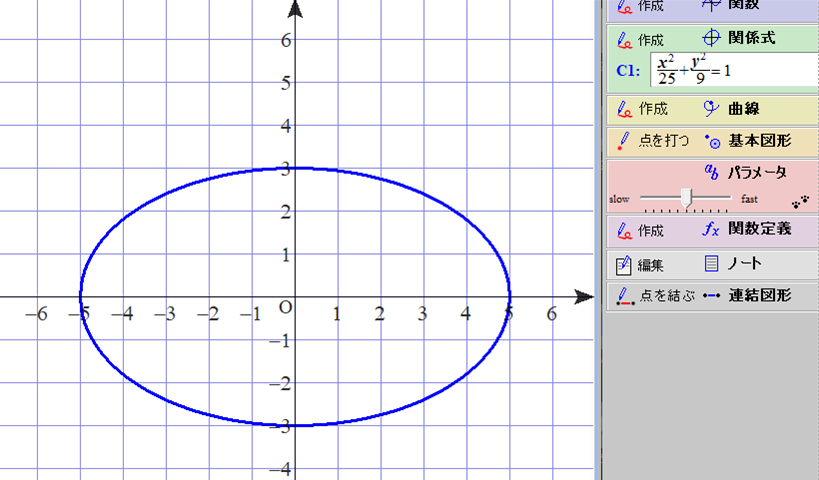
■ 上図を長軸:20cm となるまで拡大コピーして,プラ板に貼り,カッターナイフでだ円を切り抜きます.

■ 最後は,切り抜いただ円のプラ板をコーンに被せます.ほぼほぼのピッタリ感を確認できますね.


<補足>
■ 次回のテーマは「イメージ力を高める」(予定)です.イメージ力が貧しいと,算数・数学=暗記 になりがち.
■ にほんブログ村のバナーをclickしていだだけだば幸いです(最初:左,次:右).



数3で立体の断面積求めるときに習いました。
コメントありがとうございました.数Ⅲで扱いましたか.
立体の体積や断面積を求めるには,通常,積分を用います.その際,積分計算の前提として,対象となる立体の図(スケッチ図)を描く必要がありますね.
そこでケッコウ苦労します.PC画面等できれいな図が提供されますが,テスト等ではやはり「自力」で描かねばなりません.
ところで,逆に質問を一つ.今,大学では面積や体積の問題(求積問題)はあまり登場していませんよね.高校までの中心的問題はどこへ行ったのでしょうか.