公式 ⇒ with”イメージ”
数式&公式はだいたい”無色・無味乾燥”です.したがって,そのまま平板に解説する ⇒ 暗記 になりがち.

■ 暗記も必要ですが,知的好奇心を抜きにした公式の”暗記術”のみを披露・駆使していますと,いずれ壁にあたります.
■ ここでは,暗記カイゼンを図るべく,公式の背景となるイメージ例を紹介します.
⇒ イメージと一体で理解する数式・公式
2÷0.1 と 0.1÷2
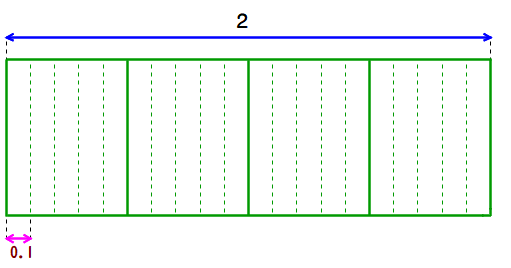
■ 2÷0.1 ですが,20÷1 と同値変形して・・・と技巧的に解説する向きもありますが,どうもピリッとしません.問題を解くだけならともかく,例えば,tan90°(=値なし)の解説のため,1/0.1, 1/0.01 などで変化の様子を確認しようとすると,トタンに思考も計算もストップするケースがケッコウあります.
■「2の中に0.1がいくつ入っているか」という,この式全体の意味をイメージ図とともに理解して,20ヶと直感的に答えるようにしたいものです.つまり,計算は不要としたいものです.
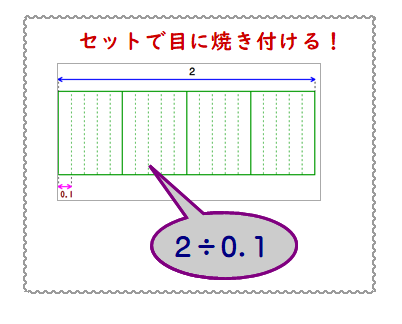
<提案>テストで「2÷0.1 を計算しなさい.イメージ図も書くこと」とすることをオススメします.「答えが合えばいいだろう」というタイドを正すには,子どもを責めてもダメ.リーダーの姿勢が反映します.
■ 次に,0.1÷2 です.「0.1 の中に2がいくつ入っているか」という問いかけにすると,答えに窮しませんか? 強引な理屈も成り立ちましょうが,小学生にはムリでしょう.
そこで,単純に「0.1を2つに分ける ⇒ 0.05」でよいのではと考えます.
つまり,2÷0.1 ⇒ 1単位量計算 , 0.1÷2 ⇒ 分割分数 という対応です
(参照) 「分数:やっぱり難しい」
比例は”with相似図”
■ 相似は中3数学で扱いますが,比例を解説する際,大いに先取りしませんか!
理由は,①授業は「教科書を」ではなく「教科書で」指導するもの,②比例計算を図抜きに説明するのはまったく以て非合理.比例という機能を相似図で補充説明をすることは,効き目ある”先手”となる からです.
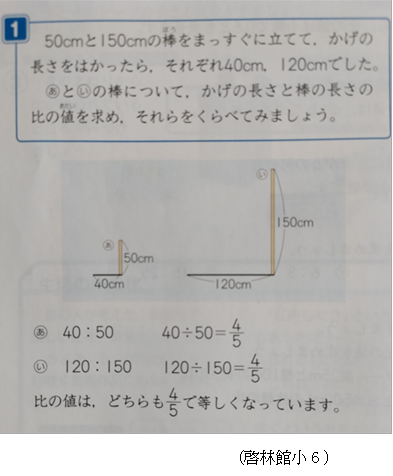
実際,教科書でも”フライング”的に扱っています.下図の例では,2つのL字形が実質,相似形として説明抜きで示されていますね.
■ 次は直線の方程式の基本公式です.

■ この公式はすこぶる評判がよろしくありません.文字数が多いことも大きな理由でしょう.twitter上でこの1ヶ月で見つけた”苦情”です.
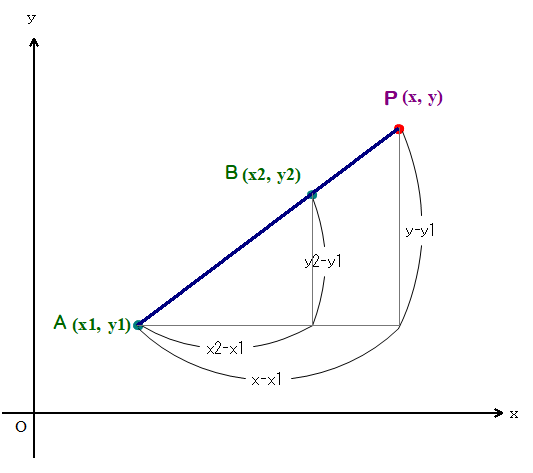

■ ②式は,相似比一定そのものズバリですから,上図とともに理解し,身に付ければよいですね(つまり,①は不要!).
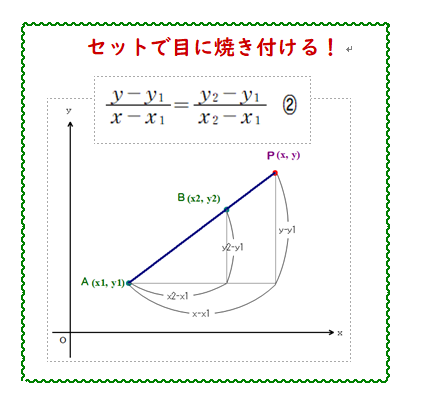
なお,

<補足>
■ 小中高連携の意味ですが,進度や履修の確認程度で済んでいないでしょうか?教材観の一致が本質です.今回は主に比例を取りあげました.
■ 次回は,「命題推理に挑戦」です(予定).公務員試験の中で,判断推理辺りが最も差が付くとの声がありますので,取りあげてみます.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).