球の体積公式,どう扱う?
球の体積Vはrを半径として $$V=\frac{4}{3}πr³$$と示され,中1で習います.
■ 球の体積公式(以後,球Vとする)は,中学生には「証明はしない・できないが,計算はさせる」という何とも扱いにくい公式ですね.”~と知られている“定理の代表です.
正式には高校の数Ⅲで学びますが,数Ⅲは選択科目であり,履修率はおそらく10%未満かと.つまり,大半のヒト(国民)にとって,球Vは,13歳前後で紹介され,後は入試や就職試験等で公式を思い出すくらいの付き合いになります.
“~と知られている”定理
■ 円の面積公式:S=πr² は,小6で登場し(πとして3.14を用い,球体積公式に比べやや詳しい説明がされている),球Vと同様に,正式な証明は数Ⅲとなります.
ただ,中3で三平方の定理を学び,高校でも三角比など,円の方程式とは絶えず接点がありますので,S=πr² とは親近感があるようです.

■ 対して,球Vは,結果が天下り式に紹介され,”そこで終える”運命の定理です.
下手をすると”この公式,覚えておけ“的な処理がされかねません.
やはり,気を遣うべきタイプの定理ですね.
■ 球Vについては,かつて,京都大学名誉教授岩井齊良(アキラ)氏(故人)が数学セミナー(or数学教育誌?)上で解説したことがあります.論の中心は,球Vへの唐突感を抱いていること,特に4/3という数値係数の背景についてでした.本稿は,氏の背景解説をベースにしております.
係数4/3はどこから?
■ 簡単にするため,半球で考えると,その体積は $$V’=\frac{2}{3}πr³$$ です.
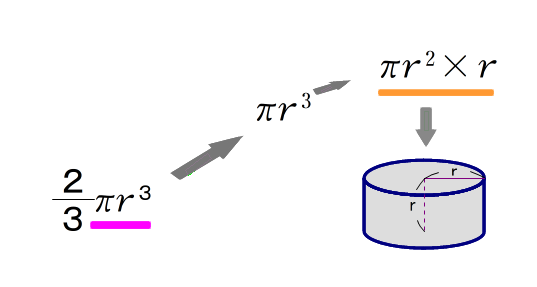
■ 上図で,πr³ は円柱V₀の体積を表していますね.
つまり,半球の体積=円柱V₀の 2/3倍 になる ことを示せばよいワケです.
ここで $$ 1=\frac{2}{3}+\frac{1}{3} $$ ですから
⇒ V₀の1/3倍の体積を加えると円柱V₀になる
⇒ 1/3 で思いつく立体は何でしょう?
そうですね.半径,高さ: r の円すいの体積が相当します.
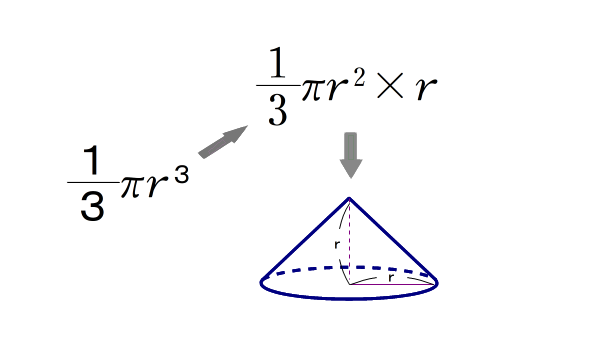
■ そこで,次のような図式(等式)が成り立つことが推測されます.
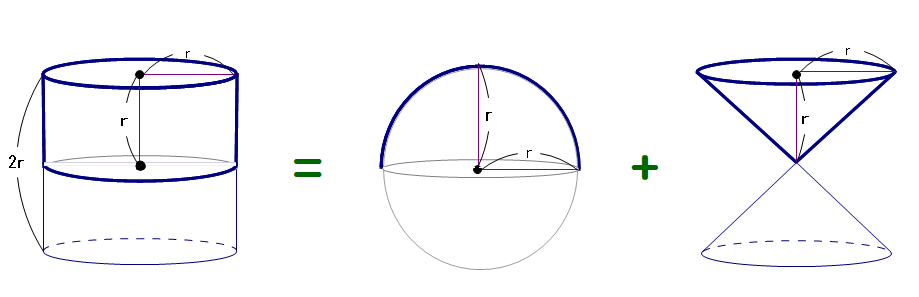
■ 図で,もし半球の体積が2/3πr³ ①と仮定すると,円錐の体積は1/3πr³ ②ですから,①+②で,3/3πr³, つまり, πr³③ となり,③はちょうど円柱の体積をしてしているワケです.
■ 実際,その仮定が成り立つことを示しましょう.
3つの立体:円柱,半球,円すいを図のように地面(水平面)に置き,地面からの高さhの水平面で各立体を切断します.
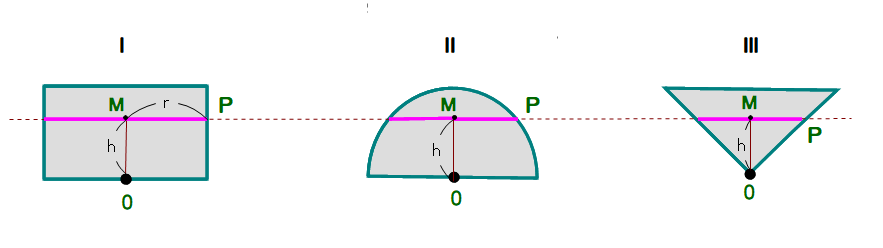
■ 上図で各切断面(S₁, S₂, S₃)はそれぞれ半径MPの円となります.
Ⅰ・・・ S₁=πr²
Ⅱ・・・ MP²=OP²-OM²=r²-h² ∴ S₂=π(r²-h²) ①
Ⅲ・・・ MP=OM=r (←高さと半径が等しい円すい) ∴ S₃=πh² ②
①+② より,S₁ = S₂+ S₃ が示されました.
つまり,高さhにおける切断面の面積がつねに等しい!
⇒ ここで,カバリエリの原理という法則があります.
カバリエリの原理

2つの立体を地面に平行な平面で切ったとき,切断面積がつねに等しいならば,これらの立体の体積は等しい.<カバリエリの原理>
■ 上図は切断面が2つとも円(500円玉)ですが,面積さえ同じならば切断面はどんな図形でもよいのです.
したがって,円柱と(半球+円すい)でもokとなります.
■ まとめると,半球の体積=円柱の体積ー円すいの体積 となり
半球の体積は $$V’=\frac{2}{3}πr³$$ が示されました.
■ 以上,振り返りますと
Ⅰ 円すいの公式:1/3πr³
Ⅱ カバリエリの原理
が認められたものとして,球の体積公式を導いてきましたが,Ⅰ,Ⅱもやはり証明抜きの「天下り公式」です.
しかし,Ⅰは球の公式と比べると唐突感は弱く,Ⅱは直感的にナットクしやすいと判断します.
このようなを踏まえて中学生には
⇒ ⅠⅡを基に,Ⅲを導く
⇒ 数学は,論の積み重ねで構成されていることを理解する
ことを期待します.
くり返しますが,問答無用の天下り公式の伝授は罪です.
<補足>
■ 次回テーマは「筆算」(予定)です.いまさら筆算でもないでしょうが,筆算の原理を今一度確認しましょう.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


