13日(金)は年に何回ある?

“学習の進んだ子ども”の第3弾です.ある日「今日は13日(金)だね.年間に何回くらいあるのかな.ない年もあるのかな」とつぶやいたところ,数日後,T君(当時高1)がレポートを提出してきました・・・.
“3昔”も前のことであり,また,レポートのママ公表についてT君本人の了承を得るのも実際的ではなく(理由は後で),レポートの趣旨に沿って「13日(金)~」の解説をします(下はレポート冒頭の一部).
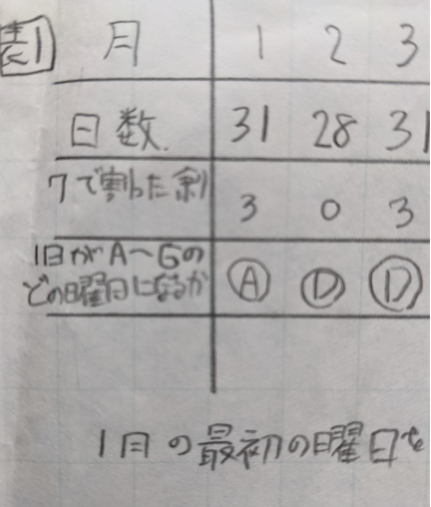
平年の場合
■ 次の表(下段)を見てください.1/1をA曜日とすると,1/2から1/7まで,Aの次曜日BからGまでが順に対応します.
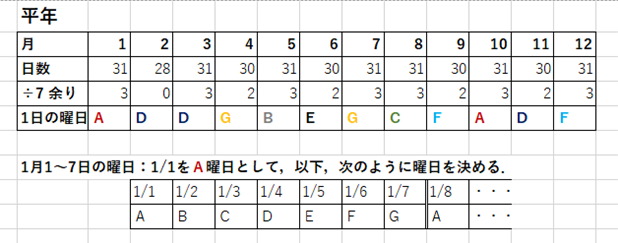
<表の見方>
■ 例:2月の欄で4段目がDのワケ・・・1月は31日 ⇒ 7で割ると余りは3 ⇒ 2/1の曜日はAから3番目 ⇒ 1/4の曜日,つまり,Dと一致します.以下,3月以降も同じ理由をくり返し,12月の欄4段目がFとなります.
<表からわかること>
■ 各月の1日は,A~Gいずれかであり,この中には日曜日が必ず含まれています.なぜなら,A~Gは,1/1~1/7の曜日と一致しており,どれかは日曜でなければならないからです.
■ “1日が同じ曜日”である月
① (1月,10月),(4月,7月),(9月,12月)
② (2月,3月,11月)
■ “1日が同じ曜日でない”月(単独月)
③ 5月,6月,8月
■ 「13日(金)」の登場回数
例1 4/1 が日曜の年は,4月と7月の計2回.他の月にはない
例2 3/1 が日曜の年は,2月と3月と11月の計3回.他の月にはない
例3 5/1 が日曜の年は,5月の1回.他の月にはない.
うるう年の場合
■ 表作成は省略しますが,上記①~③の内訳は,各月の入れ替えはあるものの,ほぼ同様のバランスで分類がなされます.
まとめ
平年・うるう年にかかわらず,年間の中に「13日の金曜日」となる月は必ず存在し,その出現回数は,年1~3回である
■ 本レポートでは,整数論の合同式等の登場はなく,もっぱら割り算を駆使した論述となっています.つまり,事象の分類能力が本テーマの核心部分であり,これは学年や教科書を超えた”センス”にかかわっています.したがって,T君は,中学生(あるいは小学生)のときでも,同じ論述ができたと断言します.
■ 今日であれば,自由研究や課題研究,探究活動等を通して,広く校内外で「日の目に当てる」ことも可能な内容でもあります.
T君のこと・T君へのおわび
■ T君は,当時,地域で有名な「将棋名人」でした.学校祭の折,「10人同時対面勝負」をやり,口の字型に並んだ一般人10人と,自身がクルクル回りながら対局し,見事全員に勝ったときは,どよめきが起きました.
■ その後,T君は東大に進学し,将棋部でも大いに活躍したものと想像します.
■ T君からレポートを受け取ったあと,誠実に吟味・評価することを怠り,今日まで「3昔」の時が過ぎてしまいました.私自身の力不足と余裕の無さに原因があり,T君が本blogに触れることはないとは思いますが,この場でお詫びいたします.
■ “学習の進んだ子ども”との出会いは,スポーツや芸術と同様に,大いに歓迎すべきことであり,その”才”の伸長ため,環境改善に努めることが周囲の大人の役目であると,再・再認識している昨今です.
<補足>
■ 次回テーマは,「宅急便のサイズ料金」(予定)です.コロナ禍の中,宅急便の利用が増えました.「120サイズは○○円」といった料金表が目に入りました.直方体3辺の長さの和:120cm内をいいます.分かり易い基準ですが,数学的にはどうなのでしょう.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).