モンティ・ホール問題に挑戦(前編)
直感 vs 論理 … 両者の解法を比較できる適例として,この「モンティ・ホール(※)問題」を挙げます.
※モンティ・ホール:アメリカの名司会者.かつて,ある番組で本問を紹介し,全米中で数学者も巻き込んでの議論が沸騰したとか.
■ 3つのドアがあり,1つのドアの後ろには新車が,残りの2つのドアははずれ(番組ではヤギ)です.
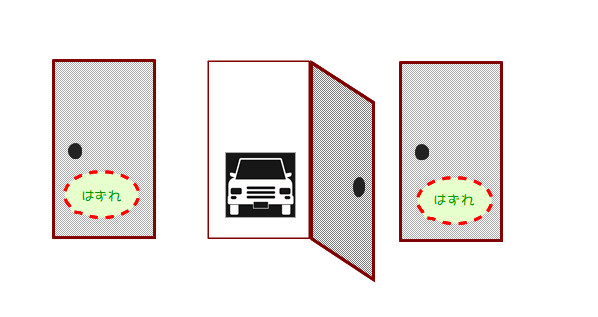
Q1 モンティは次のようにあなた(プレイヤー)に問いかけます.
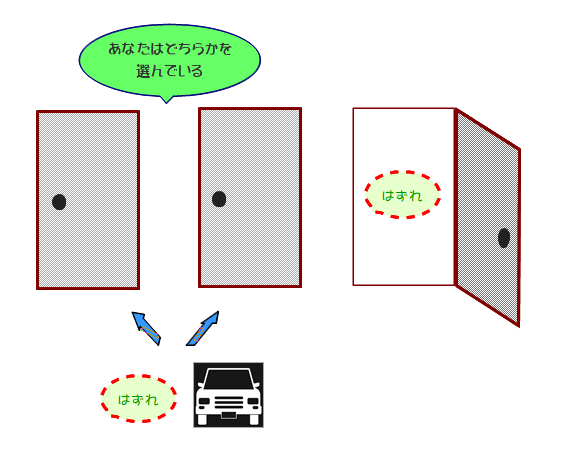
Ⅰ あなたは,適当に1つのドアを選んでください.
Ⅱ わたしは,残りの2つのドアのうち,はずれドアを開けます.
Ⅲ すると未開のドアは2つですね.
あなたは最初に選んだドアを
① 変更しない または ② 変更する
としてよいとします.
さて,新車を選びたいあなたはどうしますか.
直感による解説
A1 未開のドアは,プレイヤーが選んだドアも含めて2つある.
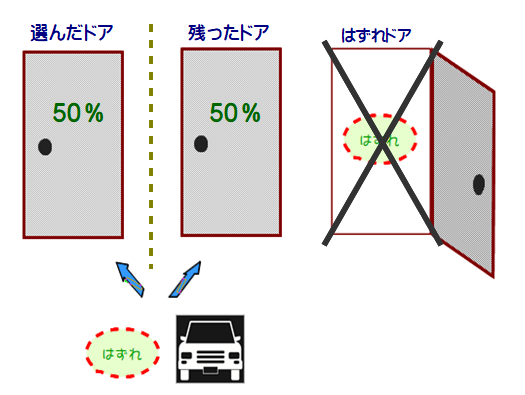

■ どちらかは必ず新車の入っているドアなので,両方ともその確率も50%だ.
したがって,そのまま「変更しない」としてよいだろう.
■ なかなか説得力ある解説です.当たる確率は半々だから,「まぁ,どっちでもよい」ということですね.さて,次の解説はいかがでしょう.
論理(理詰め)による解説
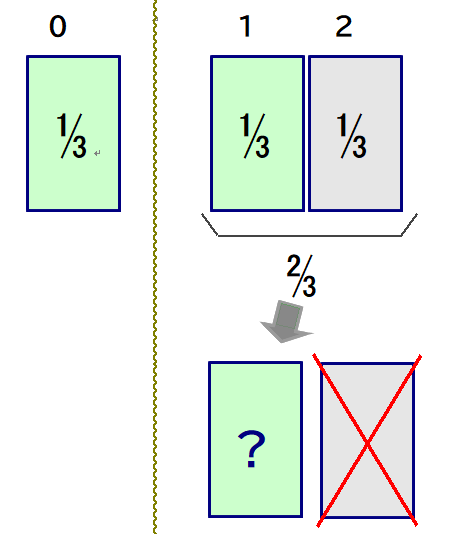
A2 プレイヤーが選んだドアを仮に No0,他のドアをNo1,No2 とする.当然各ドアの新車当たりの確率はすべて1/3 である.
すると,No1, No2 は,
①2つともはずれ
②1つが当たり,1つがはずれ のいずれかになる.
司会者モンティは,ルールにより必ずはずれドアを開く.もしそれがNo2 の場合,はずれが判明したのでゲームの舞台から退場となる.つまり,ドアNo2は”消えた“として扱ってよい.

結局,No0 と No1 のみが残る.
ここで,それぞれの当たる確率について
・No0 の当たる確率は 1/3 で変わらない
・No1 の当たる確率はどうか?
⇒ 実は,2/3 になる.
<理由>この 2/3 が本問の核心部分です.
(解1)このゲーム全体の確率は1で,No0 の確率1/3 である(これは動かない事実です).すると,No0 以外の確率は,1-1/3 =2/3 となる.
少し数式を用いると次のようになります.
(解2)No0,No1, No2 の確率をそれぞれ p₀,p₁,p₂ とすると
p₀+ p₁+ p₂ =1 ① であり,当初は,p₀=p₁=p₂=1/3 ② であった.
ところが,プレイヤーがNo0 を選び,モンティによりはずれのNo2が開かれる
⇒ p₀=1/3 であり(不変),p₂=0 である(はずれドアは絶対に選ばれないから)
よって,①より 1/3+p₁+0=1 ∴ p₁=2/3
答 結局,No1 を選ぶ(=ドアを変更する)方が,No0 を選ぶ(=ドアを変更しない)の2倍当たる確率となる.よって,ドアは変更すべきである.
注:なお,No1をはずれドアとした場合も同様の結果となることは明らか.
解A1 (50%対50%) のどこがおかしいのか?
■ 「でも,やっぱり解A1(50%対50%) の方がシンプルでわかりやすい」という思い・疑問を持っている方,少なからずおりますね.
解A1の間違いは何でしょうか?
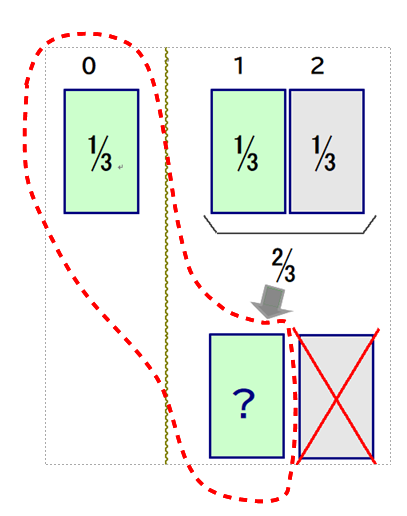
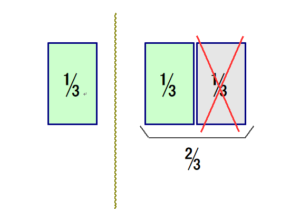
■ 図で赤点線で囲まれた部分の2つのドアに注目しましょう.
「どちらかのドア1つに必ず当たりがあるのだから,その当たる確率は,”50%対50%” で,どっちを開けてもソントクなしになるだろう」
一見,説得力に富む解説ですが,
あり得る場合(場面)を列挙して「列挙例= すべて同一確率を持つ」と解釈しています.
本問で言えば,登場するドアは,No0とNo1 のドアです.この2ドアを「列挙」しました.
列挙例が2つだったので「機械的に50%を当てた」だけであって,それぞれの「ドアが持つ確率」の違いを考慮していないのです.

■ 例えば,コイン投げでは,表・裏が出るとして話が進みますが,ある程度の厚さがあるコインだったら「立つ」という場合も理屈の上で全面否定はできないでしょう.
すると,場合は{表,裏,立つ}の3とおりです.しかし,場合が3つあるからと言って,一律に1/3(33.3%)の確率を与えることはしませんね.
つまり,複数場面があるということと,それらが即,”対等に・平等に“起こることには必ずしもならないのです.
それでもナットクできない方へ
■ 「実験」で確認することにします.この場合,理科の実験とは少しやり方が異なり「統計的な実験」になります.その結果から理論的確率の正しさを体感することにしましょう.
この続きは後編で.
<補足>
■ コインが「立つ」ことについて,「あり得ない」「無理筋」との声もありそうですね.
カミさんが500円硬貨を集めています.あるとき,たまたま落として転がった500円玉が最後,立ったママ止まったそうです.したがって,この一例をもってしても確率は「完璧にゼロ」とはならないのです!
■ 次回テーマは本blogの「後編」です(予定).エクセルによるモンテカルロ法を用いて統計的確率を求めましょう.
■ にほんブログ村のランキング(数学教育)にかかわって,バナーをclickしていだだければ幸いです(最初:左,次:INした先で右).