モンティ・ホール問題に挑戦!(後編)⇒ 理論が直観に勝る
~(中略)~ 正解は「(ドアを)変更した方がよい」なのですが,解説をみてもシャクゼンとしない向きがあります.こういう場合は,”統計的確率”の出番です.
■ モンティ・ホール問題を再確認しましょう.
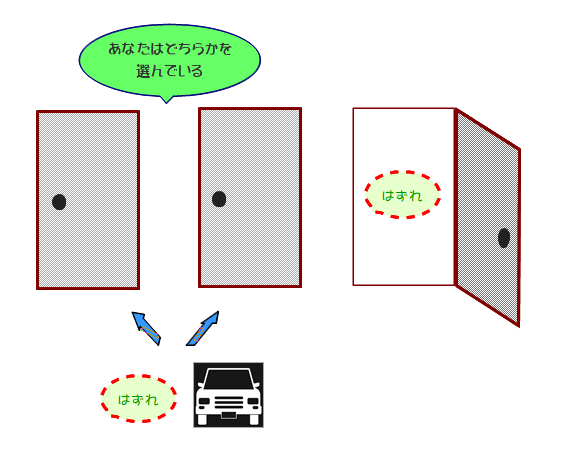
■ 3枚のドアの陰には,当たり(新車)ドア1枚はずれドアが2枚あり,あなたは適当に1枚選びます.
次に.司会者モンティは残りの2ドアのうち,はずれドアを開きます.
そしてあなたに問いかけます.最初に選んだドアを変更しますか,しませんか?と.
大別して2とおりの「解答」
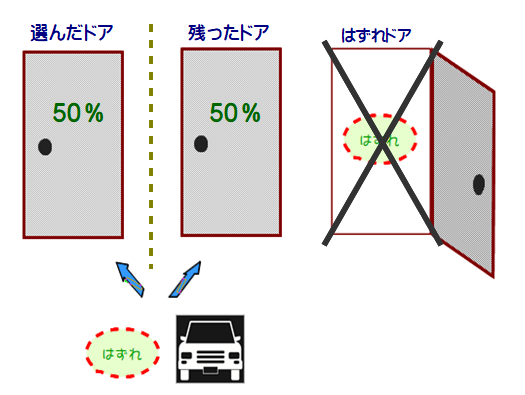
■ a:「左図のように,当たりのドアはどちらかなので,その可能性は50%ずつ.したがって,ドアは変える必要はない」
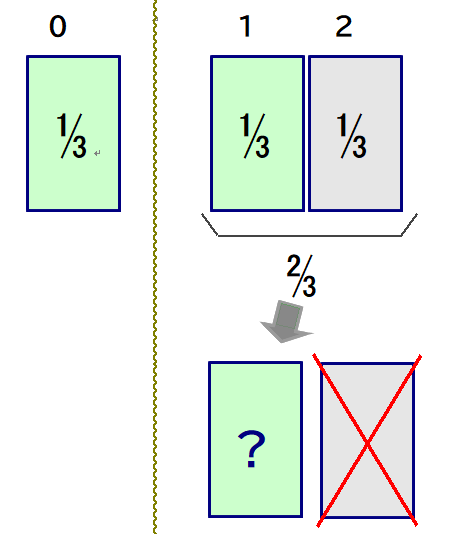
b:「右図のように,最初に開けたドアの当たる確率は1/3.残り2ドアで当たる確率はトータルで2/3. そして,はずれドアが開けられたため,そのドアは除外され,残ったドア(?マーク)の当たる確率は2/3になる.よって,ドアは変更した方がよい」
という2見解です.
■ 前編で,見解bを正解として解説しましたが,どうもシャクゼンとしない声があります.実際,アメリカでは数学者も交えての大論争になったそうですから.
モンテカルロ法で決着をつける
■ 数学では答は一つ(数学の魅力).それがヒトにより0.5 と 0.666…に見解が分かれてしまう!
これは数学ではメッタにないこと.それもごく身近な例で示されますので興味引かれます.
■ 数学的確率①とは,理論(計算)で求められる確率です.2人の誕生日が一致する確率や,サイコロを振って5の目が出る確率1/6も「まぁ」該当します(正確な作りのサイコロ).
■ あるコトをN回くり返し(試行),そのコトが起こる回数をr とするとき,r/N を統計的確率②といいます(野球における打率など).
Nがかなり大きい数なら,①と②の確率は限りなく近づきます(大数の法則)ので,モンティ・ホール問題でも適用させてみましょう.
■ 学校なら多くの子どもたちに参加してもらう手もありますね.ここでは,シミュレーションを乱数を用いて行う方法(モンテカルロ法)を取り入れました.
本問をexcelのRANDBETWEEN関数などを用いてシミュレーションしてみました.
■ 操作イメージ
① 3枚ドア(背面にNO5,6,7と書く)を順不同にセット(当たりドアをNO5に固定して可).
②プレイヤーがドアを選ぶ ⇒ ドア番号(セルD3,4,5…の数)で示す
③司会が,はずれドアを開ける
④プレイヤーは,残ったドア2枚から一つを選ぶ
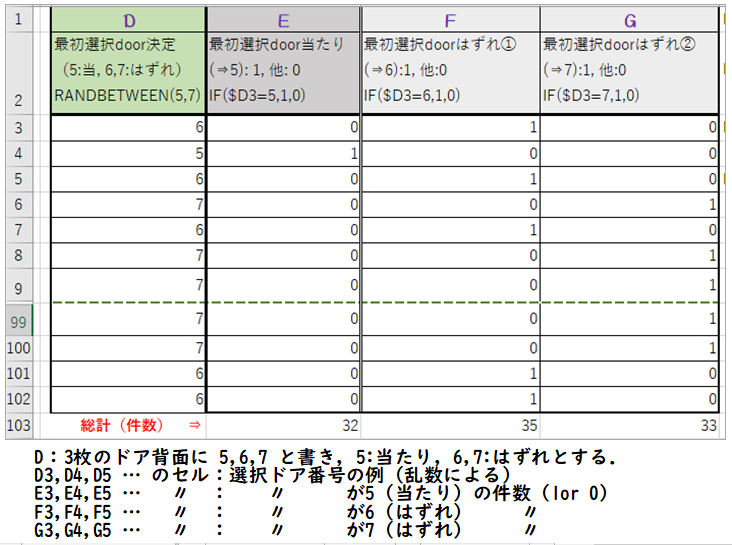
(注)当たり(はずれ)で{5,6,7}を使用した理由(通常0,1,2やa,b等を用いる)⇒ 件数をカウントする際,数:1を用いると関数式がシンプルになることと,記号:1との混同を避けるため
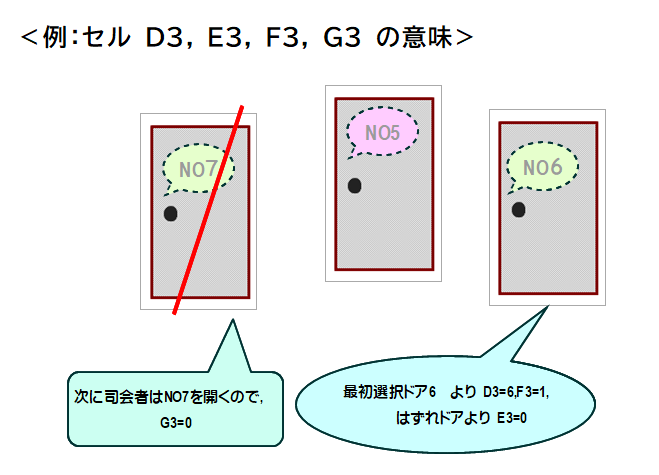
■ 上図の解釈
NO6ドアを選択したプレイヤーは,NO5ドア(司会者は絶対開けない)との2択することになり,この場合,プレイヤーはドアを変更することが有利になります.
⇔ この内容は,F3=1 という式で表されています.
excel 表から読み取る
■ 乱数を発生させて100とおりについて集計しました.
① 最初選択ドアが当たり(NO5):32%
② 〃 はずれ(NO6):35%
③ 〃 はずれ(NO7):33%
つまり,①:変更しない方がよい 32% , ②③:変更する方がよい68%
よって,プレイヤーは,ドアを変更した方がよい,となります.
<補足>
■ 本問では,ドアを100枚にするなどして話を展開する向きもありますが,ルールがやや「妙」な感じがします.つまり,残り99枚のドアからはずれドア98枚を開くというルールは不自然です.やはり本問は3枚だからこそリアリティがあり,考えようという意欲が湧くのでは?
■ excelの乱数機能によるシミュレーションにはケッコウ難儀しました.操作内容の式化がタイヘン.いろいろな文献やサイトを参考にしました.
■ 次回のテーマは「式変形を数学的思考から観る」(予定)です.平方完成など,式変形のための式変形になっていませんか.
■ にほんブログ村のランキング(数学教育)にかかわって,バナーをclickしていだだければ幸いです(最初:左,次:INした先で右).