先生,周りみんなの三角形が皆ベツベツなんですけど…
A大学教育系学部の学生たちが出前授業として高校で数学を担当(復習)しました.その一場面からの話題提供です.多少脚色をしていますが,本テーマの顕在化のためですのでお許しください.
最初の「問いかけ」が流れ全体を左右します

■ 以下,担当学生Tさんの出だしの発言です.
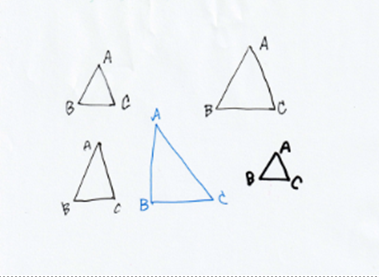
① では突然ですが,三角形ABCをノートに描いてください.
② 描いた? では,周りの皆さんの三角形と見比べてみて.
③ ハイ,協力ありがとう.どう?
そうですね.〇さんがつぶやいていましたが,大きさも形もバラバラです.正三角形や二等辺三角形が多い傾向かな.また,小さい三角形がちょっと多いぞ.これからはもっと大きく描くように.大切なことですよ.
④ ところで,何でみんなの三角形はバラバラになったのですか?
ホゥ,条件不足ですか.ナルホド.では,ここにいる皆さんが同一の三角形を描きたいときは,どんなことを言えばよい?・・・(やりとり略)・・・
⑤ 今,ピリッとする言葉があったね.何て言いました?
「三角形の合同条件」「三角形の決定条件」ですね.中学校時代の記憶が鮮明になってきたかな.
どんな内容だっけ?あいまいそうな空気もありますね.
では,各グループで共通の理解を「確実」にしてください.全員残らず,ですよ.後でチェックします.(中略)
⑥ さっき再確認した3つの三角形決定条件のうちどれかに該当すれば,いつでも・どこでも・誰が描いても皆同一の三角形ができる,というワケ.
条件さえ合えば,江戸時代に新作が描いた三角形と,今,中国の少年チンが描いた三角形が同一になります.

⑦ ところで,今日のお相手(問)です.ざっと見て.教科書の例題クラスです.
問 「…三角形ABCにおいて,sinA:sinB:sinC=7:5:3 である.このとき,…」
まず,三角形の図が描かれていないね.小中までと違って高校数学では自分で図を描かなきゃいけないことが多いんだ.
では,大まかでいいから描いてみよう.今度もさっきみたいにバラバラの図になるかな~
(以下,略)
復習の仕方:既習内容 ⇒ Ⅰ 時系列でなぞる Ⅱ 別視点から再確認する
■ 可能ならばⅠ式は避けたいですね.特に,中高生にとっては,既視感(デジャブ)があり,同じように習ってその結果,理解が深まらず「今がある」ワケですから,数学への不信・不満もあっても不思議ではありません.分数が分かってない高校生に,算数のテキストで挑戦させてもよい結果は生まれないものです.
■ 学生Tさんは,
突然,全員に三角形を描かせました.
結果,(当然ながら)皆,ベツベツの形となったワケです.
その事実を互いに確認・体感させて
本題の意味理解→解決 へと流れを作っていました.

三角形が決定する…よく耳にします.リーダーも口にします.また「~が決まる」という表現は数学ではフツーです.
しかし,「決まる」に対してヒトビトが抱くイメージはどんなものでしょうか?少なからずのヒトは抽象的な理解程度に留まっていると見ております.そこで次の手を
⇒「決まらない」例を体感してから,その対極の「決まる」意味を再認識する
この発想&手立ては数学を学ぶ上で有効です.
■ もし担当した学生が次のように展開したらどうでしょう.
① この問ですが,まず題意を踏まえて三角形を描く必要があります.図がイメージしにくいですね.
ところで,中2で三角形の合同条件ってやりましたね.どんな内容でしたか.どうですか?
ハイ,〇□さん.(中略)
② どことなくあいまいな部分もありそうですので,各グループごとで話し合ってください.
(以下,略)
Tさんと比較して,自身の結論ありきの展開で,論理の流れが悪い上に,記憶の再生を前提としているため,効果ある復習になっていませんね.残念!
また,グループ学習への指示も形式的で「学び合い」には程遠い状態です.
こんな例も
■ 本blogでは復習の在り方についてこれまでも話題にしてきました.
Q 1÷1.414 を計算してください.
A 解Ⅰ まともに割算する ・・・
解Ⅱ 1.414≓√2 ∴ 与式≓1/√2=√2/2≓0.707
分母の有理化を復習する際,本Qのような例と対面させて,有理化の意味と意義を理解してから,計算練習に入りたいものです.
「平方して3になる正の数を√3とかく」.だから,(√3)²=3
確かにそのとおりで国語の領域なのですが,これを復習してもピンときていない多くのヒトと出会ってきました.
ときには,逆向きからのアプローチをお薦めします
⇒ 「1.732×1.732 のおおよその値を求めてください」
実際に計算し始めるヒト,いると思いませんか?いるんですよ.
Q 分子の有理化の復習はどうしますか?
<補足>
■ A大学の学生派遣事業(数学教育研究室)・・・近隣小中高学校への「学生出前授業」の一つとして実施されており11年目を迎えています.課題も多々ありますが,この手の事業としては異例の長さかと.
習う側,指導する側の双方にとって「苦手」とする分野に焦点を合わせているところが通常の教育実習との違いです.たとえば,小学校の分数(単位量),中学校の文字や関数,高校の三角比が「挑戦」分野です.もちろん,学生主体ですから「復習」の形をとります.
■ 次回テーマは「こだわる」(予定)です.今や(数学で)「こだわるヒト」は絶滅危惧種かも.
■ にほんブログ村のランキング(数学教育)にかかわって,バナーをclickしていだだければ幸いです.↓