立方体を回転させると…
立方体の回転もいろいろですが,中心を通る対角線を軸にして1回転してできる立体を話題にします.立方体という見慣れたモノを用いてはいますが,ケッコウな内容で手強いです.
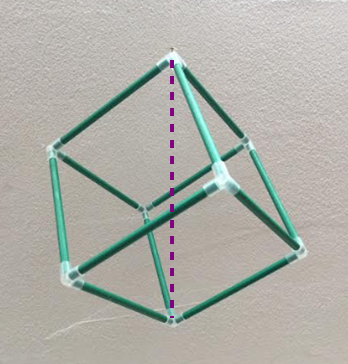
■ 写真では一番上の頂点で細い糸がかすかに見えておりますが,立方体がぶら下がっています.この状態で立方体をクルクルと回すわけです.
■ 全体像はさておき,部分的に見ていきましょう(←”落とせそうな”ところから攻める!数学的思考の一つ).
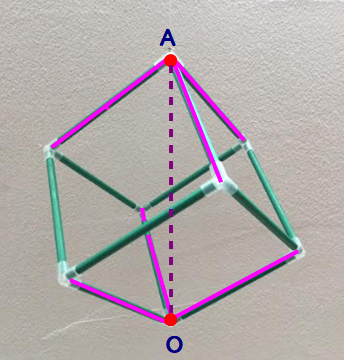
■ 図で,上の頂点Aに集まる3本の辺で四面体Ⅰができますね.
下の頂点Oに集まる3本の辺でできる四面体Ⅱと合同図形(立体)になります.
■ 四面体Ⅰ,Ⅱに底面(正三角形)を付けてみます.

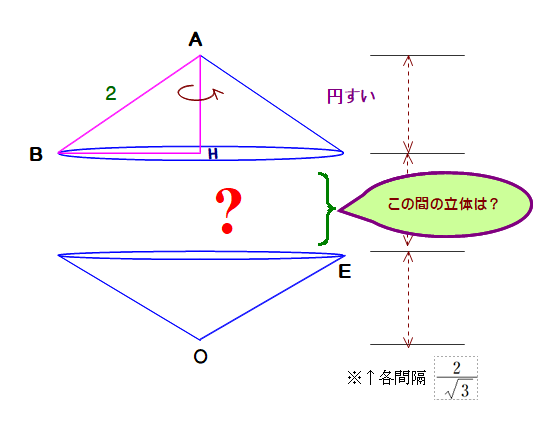
■ 図では,二つの底面が交叉するような様子ですが,目の錯覚で実は平行になっています.次の図を見てください.

■ 四面体Ⅰ,Ⅱが底面を平行な状態にして1回転します
⇒ Ⅰ,Ⅱが1回転してできる立体は?
⇒ ハイ.円すい!になります.
■ 立方体の1辺の長さを2として,四面体Ⅰを「料理」しましょう.
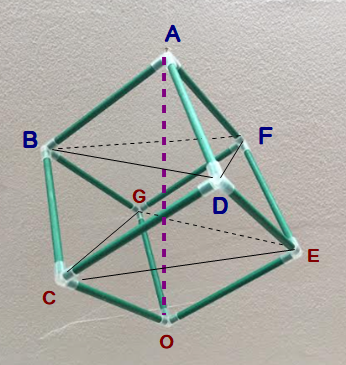
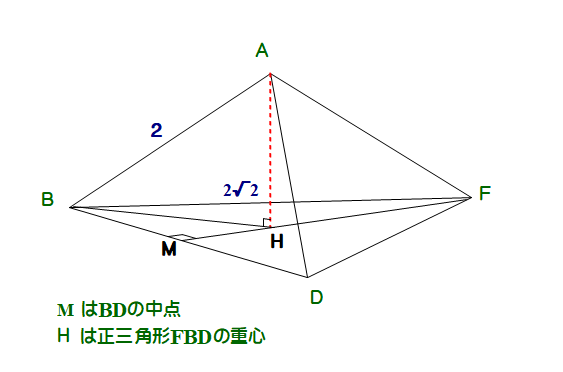

■ V1,V2 は求められました.
これで”終了”となればよいのですが「本丸」が攻め落とせておりません.
■ 実は,この残った立体の処理がやっかいなのです.
⇒ まずイメージできるかどうか.

■ 図を再掲します.回転軸AOと「ねじれの位置」にある6本の辺(緑色)に注目します.
■ 6本の内,1本おきに同じ辺となりますので,結局,求める立体は直交している左手前の2辺(緑色)だけで形成されるとしてよいことになります.
■ さらに,絞られた2本ですが,回転の向きを変える(左⇔右)と同じ軌跡となります.
結局,軸とねじれの位置にある緑色1辺だけに焦点を合わせればよいわけです.
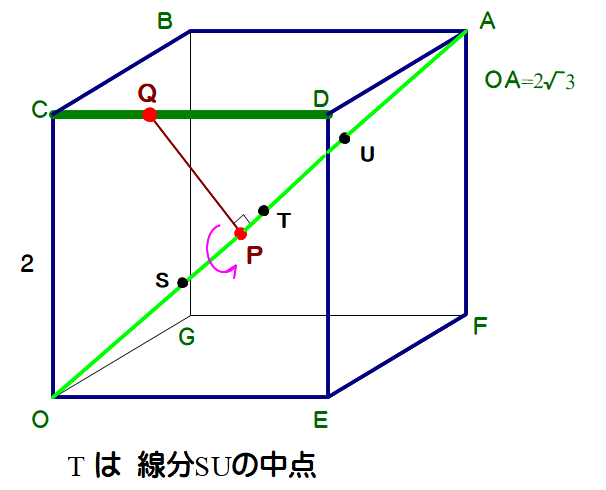
■ 図で,OS=SU=UA=2/√3 です.回転軸OAとねじれの位置にある辺CDを軸回りに1回転した様子をイメージしてみてください.
■ ナント,図のように点Pが線分SU間にある場合は,鼓(つづみ)のように中が引っ込んだ形となります.
では,ユーウツな計算式を紹介します.




<補足>
■ 今回,フレーム式の立方体を用いましたが,このような教具を自作するユトリがなく,ネットで”発見”して画像で紹介した次第です.made in china ですがよいモノです.ただ,送料と本体が同価格というのは疑問?(計2k円程度)
※「算数教材 立体図形 直方体 立方体 3D幾何学図形模型」

■ 本テーマでは計算力もさることながら「立体をイメージする」ことに重きを置きました.
■ 次回テーマは「量感upは全教科で」(予定)です.
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.