30°C+50°C=80°C とならないワケ
30g+50g=80g, 30cm+50cm=80cm はよしとして,30°Cの水+50°Cの水=80°Cの水 は成り立ちません.その「ワケ」理解はいかがでしょうか.学生も含めてかなり怪しい状況です.
■ 教材学研究第24巻「教員養成系大学生の量概念の実態と温度概念形成に向けた指導方法」(帝京科学大学 小池他,上越教育大学 高津戸)を基に話題を提供します.

量は大別して2タイプ
■ 日常よく目にする量についてですが
Ⅰ:長さ,重さ,広さ etc
Ⅱ:速さ,濃度,温度 etc
と2つに大別できます.
違いは何でしょうか?
⇒ Ⅰは,2g+3g=5g のように加えることができる量で,外延量(extensive quantity)といいます.
⇒ Ⅱは,速さ・人口密度のように加えることができない量で,内包量(implicate quantity) といいます.
※ 内包量は「2つの外延量の商」であることから,単位もそのママ km/h, 人/km² などと表す.ただし,温度の定義は諸説あり単純に「2外延量の商」では済まされないよう.しかし,後に述べるように外延量ではないことは確か.
内包量(温度)についての素朴な疑問
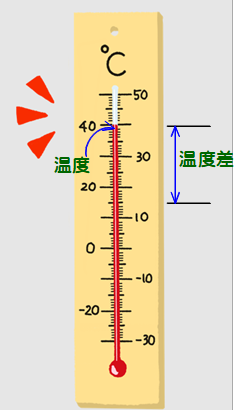
Q 温度計が40°Cを指しているとする.何らかの熱を加えて10°Cアップさせて50°Cにさせることは可能.
つまり,40°C+10°C=50°C である.これは,温度が外延量であることにならないか?
A 温度と”温度差”を混同している.また「+」の意味を”付け足す”操作に誘導している.
単位である°C について述べる.棒温度計は温度変化を液柱の体積(=長さ←管の直径が一定の場合)が示す目盛りの位置で温度を測るもの.
その際,水の沸点を液柱の最高点:100°C,水の凝固点を0°として,その間を100等分して目盛りを付けている.
このように液柱の先端の位置は温度を示し,液柱の長さは基準点からの温度変化(温度差)を示している.
したがって,40°Cの液柱の長さと10°Cの液柱の長さを加えて50°Cの液柱の長さとなるのは,線分長さの和,つまり,温度差の形式的加法であり,温度そのものを「加える」操作・演算が定義されていない.
実際,40°Cの水に10°Cの水を加えて(付け足して)50°Cの水ができるはずがなく,
40°Cの水+(何らかの加熱をして)=50°Cの水
という式ならば説明はつきそうである.※この場合の「+」は,「その状態のママ」くらいの意味
グラフでy軸(縦軸)が内包量のときは”要注意”
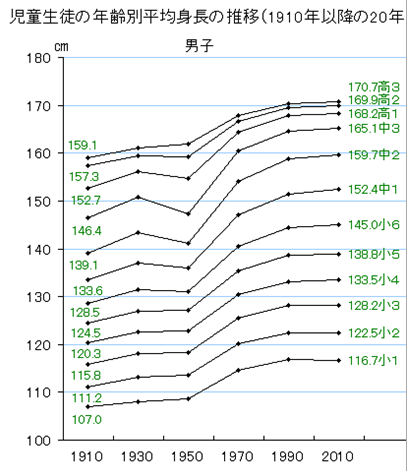
■ 図は,縦軸(y軸)が身長(cm)で外延量
⇒ y軸が長さや重さなどの外延量のときは,問題なく読み解くことができそう
しかし,以下のように,y軸が内包量のときは,数学リーダーはより慎重に・より確実に論を展開する必要があります.
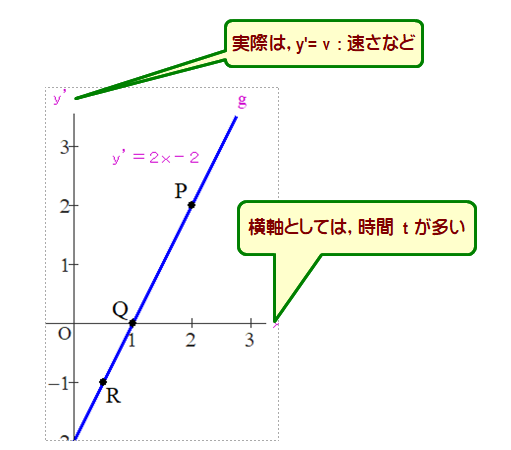
■ 図で,y軸はy’(例:速さv)であり導関数を示しています.図形的には微分係数すなわち”yの接線の傾き”をイメージできるかどうかが全体理解の「試金石」になっています.
例:点Pではy’=2 ∴ yは点Pで右上がりの状態
例:点Qではy’=0 ∴ yは点Qで(一瞬)水平の状態
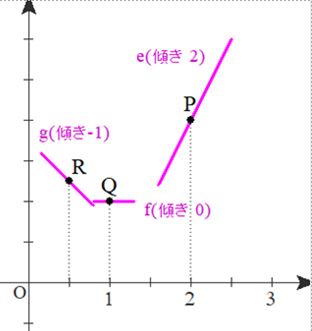
■ いろいろな点におけるyの状態を総合するとyのグラフは概略,次のようになることが分かります.
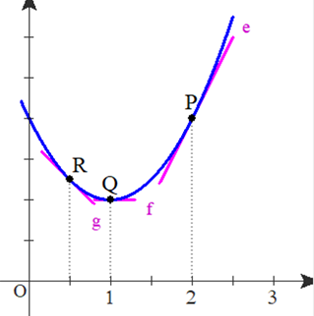
■ まとめると,y’=2x-2 よって,y=x²-2x+c (c:任意定数) つまり,yは放物線を表す.
⇒ 形式的に微積分計算ができても,イメージが伴わない計算力ではいずれ行き詰まり発展性がほとんどありません!
<補足>
■ 参考にした「教材学研究第24巻」で印象に残るdataがあります.それは対象学生91名への調査で「量概念はいつ学習すべきか」という問に対して半数前後の学生が「小学校と大学」と答えていることです.中高ではなく,小と大なのです.妙にナットクしたdataですね.
■ 次回テーマは「1当たりの大きさ(改良版)」(予定)です.ある方から意義ある提案をいただきました.
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.