「分数÷分数」 計算のナットク感はどう?
\[例
\frac{3}{4}÷\frac{5}{8}=\frac{3}{4}×\frac{8}{5}
\]


2分数の割算は「計算はできるにしてもワケはわからない」典型例かも知れませんね.
■ 過日,本blogで
をupしたところ,√6さんよりコメントを頂戴いたしました.後述しますように
2分数割算の計算ルール ⇔ 1当たりの大きさ
であり「本質」が同じですので,ここでは√6さん案をメインに話題を提供します.
Q 小6算数の問題です.
\[ \frac{3}{4}m²の壁を\frac{5}{8}dlで塗れるペンキがあります. \] \[ このペンキ1dlで何m²の壁が塗れますか. \]A (√6さんからのコメントです)

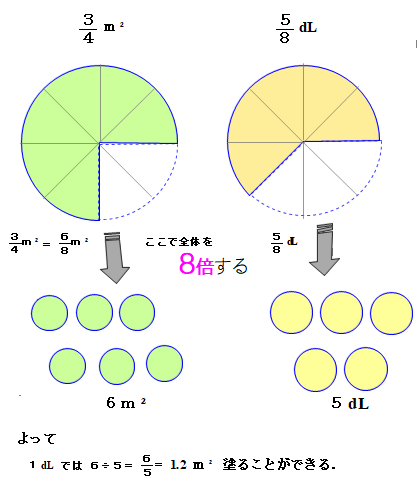
■ コメント内容を図示しました.

■ いかがでしょう.図も参考にすれば分かりやすい解説ですね.√6様,深謝します.
ところで,本問について再度確認します.
\[ \frac{3}{4}÷\frac{5}{8}で答えが求まるのはなぜか ① \] \[ \frac{3}{4}÷\frac{5}{8}=\frac{3}{4}×\frac{8}{5}となるのはなぜか ② \]■ ①について
上記コメントの流れを逆にしますと
\[ 1.2=6÷5=\frac{6}{8}÷\frac{5}{8}=\frac{3}{4}÷\frac{5}{8} \] \[ ここで,1.2=\frac{1.2}{1}(m²/dl)であることから \] \[ \frac{3}{4}÷\frac{5}{8}=\frac{1.2}{1}(m²/dl) \] よって,左辺の割算は1(dl)当たりの面積計算をしていることになります.■ ②について
\[1(dl)当たりの面積を求めるため\] \[「8倍して5で割る」操作\] \[⇔ 「×\frac{8}{5}」 と式化\] したがって \[ \frac{3}{4}(m²)÷\frac{5}{8}(dl)=\frac{3}{4}×\frac{8}{5} \] となります.2分数割り算の計算ルール
■ √6さんのコメントを基に,2分数割り算の計算ルールを代数的に導いてみましょう.

<補足>
■ 15÷3 ⇒ 3を「1塊」と見なせば15には5ヶ分入っている.これはokですね.同様に3/4÷5/8 ⇒ 5/8を「1」と見なした計算となっている! ここのナットク感を持つことが出来るかどうか.正に分岐点です.改善策の一つは「テストに出題する」ことで,答えよりもプロセス重視の空気を醸成する必要があります.
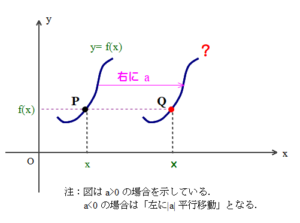
■ 次回テーマは「グラフの平行移動とその式化」(予定)です.「y=f(x)について,xの代わりにx-3 とすると,y=f(x)のグラフをx軸方向に3だけ平行移動したもの」ですが,符号が変わるワケとは?
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.