スーガクへの怨嗟①(例 平行移動の式変形)
「怨嗟(エンサ)」は少しオーバーでした.しかし算数・数学の解説で,どこかあいまいさ・モヤモヤ感が残り,積もり積もってエンサとなることはあり得ます.実際「問題を解いていくとそのうちワカルよ」などと根拠の薄い弁解しながら先へ進む授業光景も散見されます.

■ 先日,twitter上で見つけた一例です.
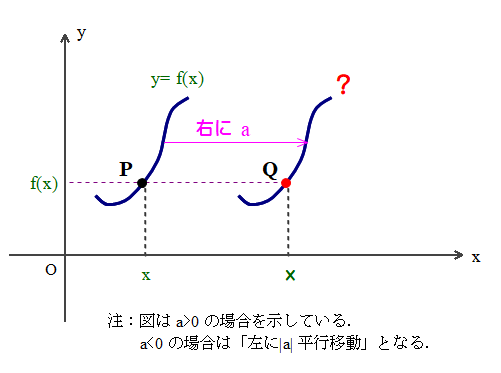
関数y=f(x)のグラフをx軸方向にp平行移動したグラフの式は,
y=f(x-p)
となります.y軸方向も同様.
⇒ 何で,x–p となるのでしょうか?x+p ならばナットクなのですが…
という主旨でしょう.
「ガチガチ」の証明
■ 次は,(たぶん悪名高い!)証明です.

数学に”恨み”を持つヒトからの声
■ 数学がわかるヒトにとっては,何に引っ掛かっているのか?と思う”声”でしょうが…
(1) 最終行で「Xをxとする」とあるが,こんな勝手なことができるのか?
また,いろいろな場面で出てくる「x軸上のx」ってというのがそもそもスッキリしない.
(2) 1行ごと論を追っていくと正しい数式が並んでおり展開もそのとおりだとは思う.しかし,全体としてのナルホド感がなく,結局,平行移動 ⇔ 逆符号 を棒暗記している.
一応の答え
(1) Xをxとする ⇒ 「Xを x と書き換える」という言い方が適切だと考えます.
ギリシア文字xは変数の象徴です.どうしてもというなら, xは別文字で表現してもよいワケ(例:aやpなど.ただ,これらは定数として登場することが多い).したがって,xと区別するため一旦Xとしたのちに,誤解がないならXを x と書き直しても構わないのです.
特に,関数を扱う場合,点(x,y) は,xとyの間に成り立つ関係が本質で,別の文字を使用しても関係式が一致していれば同一関数となります.
例:放物線 y=x² を b=a² と書き直しても放物線自体は変わりません(ただし,a,b座標軸にして).
(2) 証明自体はどう工夫しても先程の内容とほぼ同じになります.
ピンとこない,なるほど感がないということなので,具体例で補足します.
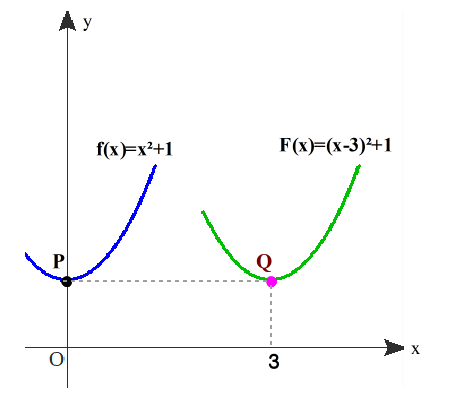
図は,y=x²+1 のグラフをx軸方向に3平行移動してできるグラフの式が, Y=F(X)=(X-3)²+1 であることを示しています.
ここで,F(3)=(3-3)²+1=1
よって,f(0)=F(3)=1 ①
つまり,F(3)を求めようとすると,f(0)の値と一致する
⇒ X=3 とすると,x=0 のときのf(x)の値と一致する
⇒ 一般に,すべての点においてXに対して3引き戻されてxとなる.
⇒ 逆に見ると,グラフy=f(x)をx軸方向3平行移動したグラフ Y=F(x)の式は
Y=F(x)=(X-3)²+1
つまり,y=(x-3)²+1 となります.
平行移動の式変形は「一貫」させる
■ 平行移動の変形は,すべての分野で通用する・させるべきものです.
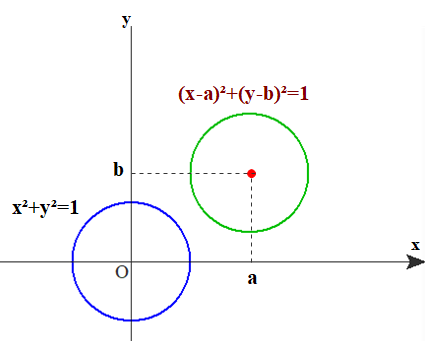
例 単位円x²+y²=1 をx軸方向p, y軸方向q 平行移動する.
⇒ x → x-p , y → y-q とすればよいので
(x-p)²+(y-q)²=1
となります.
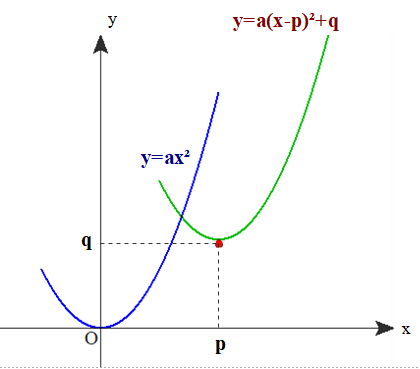
例 放物線y=ax² をx軸方向p, y軸方向q 平行移動する.
⇒ x → x-p , y → y-q とすればよいので
y–q=a(x-p)² ①
ゆえに,y=a(x-p)²+q ②
※ 一貫性に欠けメーワクな指導解説
「y=a(x-p)²+q を放物線の標準形と言います.頂点は(p, q) で,p,qに付いた符号が異なることに注意してください」
平行移動⇔逆符号 と暗記していたヒトは混乱すること必至です!
解説の一貫性という視点からは,放物線の標準形は
y–q=a(x-p)² ①
とすべきです.少なくとも②が定着するまで①は再三登場させましょう.
<補足>
■ 確かに「x軸上のx」という言い方は気になりますね.もし,日本が世界の文明の中心であったなら「あ軸上のあ」となったかな?!
■ 次回テーマは「点と直線の距離公式」(予定)です.受験数学には必須の公式ですが,根号・絶対値がつき,かつ,分数形式ですので近寄りがたい公式の一つ.
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.


