「7²+7²=98」 の活用
ごくありふれた三平方の等式:7²+7²=98 が,意外にも高校生や学生の弱点をケッコウ突きます.
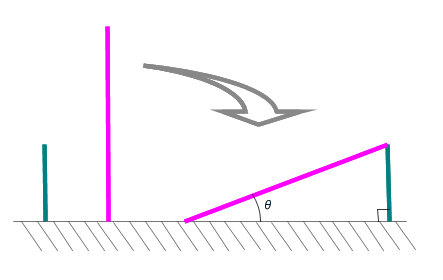
■ 図のように,短い棒aと長い棒bがあります.aを地面と垂直に立てて,bの端をaの先端部と地面に付けます.
このとき,bと地面とでなす角θを答えてください.
Q1 90cm と 100cm ⇒ θ は{①55° ②65° ③75° ④80° ⑤85° }くらい
Q2 70cm と 100cm ⇒ θ は{①40° ②45° ③55° ④60° ⑤70°}くらい
■ さて,いかがでしたか?
2問とも即,通過され「なぜこれが問題になるの?」と感じられた方は,読み続ける必要はなく,”別天地”へお進みください.⇒「坂道のθを測る」などへどうぞ.
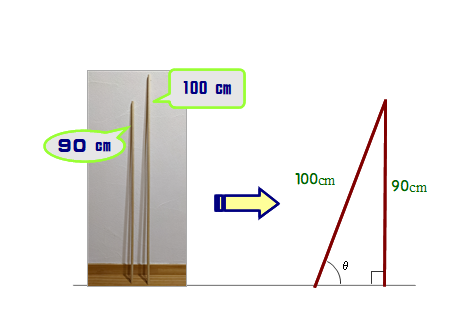
A1 ②65°が もっとも正解に近い値です.
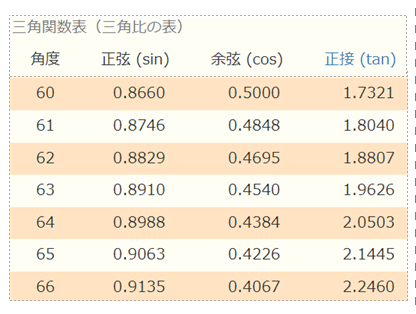
図で,sinθ=90/100=0.9
三角関数表より,sin64°≓0.8988 よって,選択肢の中でもっとも近い角度は,65° となります.
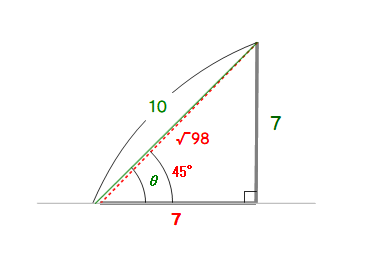
A2 ②45° が正解にもっとも近い角です.
相似形の性質より3辺を 7, 7, 10 としてよいですね.
図で,三平方の定理より,7²+7²=98 です.
ここで,98≓100,つまり,√98≓9.9 ≓10 となるので,
∴ sinθ=7/10 ≓ 7/√98=sin45°
∴ θ≓45°
テーマ設定のきっかけ
■ いかがでしたか.
Q1 では,棒が,100cmと90cmと接近した長さなので,とんがった直角三角形となって,θも90°に近い角と思った方,いませんでしたか.
Q2では,60°前後とする誤答もあったと想像します.
■ 角θ:2直線(線分)の交じり具合 ⇒ 相似比一定を基に,角を直角三角形の中に限定すると,各辺の長さの比でθは決まります.
この辺の長さと角の関係があいまいと感じます.
例 ① 100cmと87cmの辺 ⇒ θ≓60° (√3/2≓0.87 の認識がホントに弱い!)
② 100cmと50cmの辺 ⇒ θ=30° (45°という答が必ずありますね.弦の長さが中心角と比例する,つまり,100:50=90°:45° と判断しているからです).
■ たとえば,sinθ=1/√2 を満たすθを求めようとします(いわゆる三角方程式というヤツです).

■ 図1のような解答例の多さには閉口します.
√2を1.414と暗記していても,量感抜きで進めてきたヒトは,0.71の点が適切な箇所に打てないのです!.→ 「0.5と1の中点は0.75,だから,0.71はそれより下方・・・」こういった自身とのやり取りができないのです.
結局,座標点が正しくないものですから,円からθ=45°が読み取れず,30°や60°などと苦し紛れの答となったりもします.
√2,√3,π・・・量感を以て理解すべし
■ √2=1.414・・・, sin45°=1/√2 ・・・これらは,三平方の定理「7²+7²=98 」をベースにした結果です.ヒトヨヒトヨ・・・と暗記させることを否定はしませんが,もし量的な意味理解さえも伴わない強要学習が中高と共通していれば,「負の中高一貫教育」となり下がりますね.

■ 10cmと7cmの割りばしを用意して,冒頭の直角三角形を作り,その底角が約45°となることを,
①予測,②実測
させましょう.その際の順番は,①→②でなければなりません.
<補足>
■ 量感覚がプアなため,点が適切に打てず,「自身とのやり取りができない」と上述しましたが,改善のための対応策は難しくありません.定期テスト等で出題することが最短コースです.
■ 次回は,「フツーのサイコロ=正しいサイコロ?」(予定).あまり深刻に考えないで接するサイコロですが,気になります.
■ にほんブログ村のバナーをそれぞれClickをしていただければ幸いです(最初:左,次:右).