√３は文字か？

夕方頃，駅前の交流センターでおしゃべりしている高校生に”突然”問います（当方，交流センターに少しばかり関わっていますが，まぁヘンなおじさんと見られることもあるかな？ その辺は前後ヨクヨク考えて行動していますが・・・）．

1.732 × 1.732はどのくらいになる？_（※）

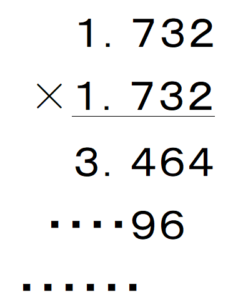
これまでの経験では，少なからずの生徒が，実際に計算しようとします．筆算やスマホの電卓使用で，とにかく，正しい答えを求めようとします．
適当なところでストップをかけて，「おおよその値でいいんだけど」と言うと，ようやく気が付く生徒がいて，「３」という反応が返ってきます．
中学生は，√３＝1.732（ヒトナミニ・・・）と習い，覚えます．必死に暗記します．

しかし，学生（理工系でも）に，sin(π/3)の値を問うと，まず，√3/2と答えますが，それは，約0.87であり， 0.9に近い値だという認識はもっていないようです．実際，いわゆる有名角（30°，45°の倍数角）以外の角と遭遇すると，お手上げ状態になる学生がおります．たとえば sin80° は 0.9 より大きく，かなり1 に近い値であると体感で理解してほしいものです．

２点指摘します

① √３ の定義が意味理解されていない．ナルホドそういうことか！と納得させるツメが甘い．上記で示した※のような問いかけの工夫が不足している．人が生きる上で，どうしても長さや重さなどの量を比較する必要性があって生まれたのが数．「２」という数字が道端に落ちていたのではない．その量（量感）を軽視することは，学びの流れと逆行することになる．

②少なからずの生徒は，√３ を量的に認識しておらず，ヒトナミニの語呂合わせ暗記で終始している．根号という新しい記号を用いた数√３自体を象形文字のようにとらえているのでは？ 学年が進み，座標平面で（√３－１，２）のような点をプロットする必要がある際にも結構苦労する．

※分数に比べると無理数はまだまだ「楽勝」です．なぜなら，2/3 は，大ざっぱに言って分割分数（２を３等分する）と量分数（0.666･･･)という２つの側面（その他，諸説があります）をもっていますので．これは小学生にとっては大変で，同情します！

 

■ にほんブログ村のバナーをClickしていただければ幸いです(最初:左,  次:右)．