(sinx)’=cosx の図形的理解
(sin x)’=cos x を体感しよう
公式により計算は一応出来るが，実のところ，意味理解は出来ていない生徒や学生は少なからずおり，微積計算でもしかりです．
微分係数 f'(a) は，定義により曲線 y=f(x) 上の x=a に対応する点Ｐにおける接線の傾きを表すのでした．つまり，右上図で，f'(a)=tanθ というわけです．
ちなみに，接線の英訳は，tangent です．
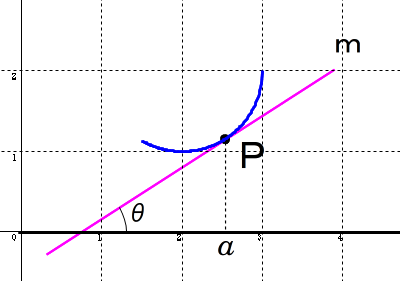
たとえば，f'(3)=1
曲線上で x＝3 に対応する点の接線は,x 軸と45°の角をなす
さらに，a をx で置き換えたものが f'(x) です（→ このあたりの臨機応変さ・自由勝手さに苦しむ生徒もいます）．
したがって，f'(x) は，曲線上の点 P(x,y) における接線の傾きを表します．
⇒ つまり，点x=x における接線の傾きです！
例：ｙ’=f'(x)=2x
微分の定義に基づいて y= sin x の導関数を求めると，複雑な計算が必要なのですが，確かに y’= cos x が導かれます（高校数Ⅲ教科書）.
それにしても，sinの微分結果がcos とは！ 何とも不思議なコトだという思いを抱かれた方も多いのでは？ この不思議感を払拭すべく，以下のように図形的解釈を試みました．
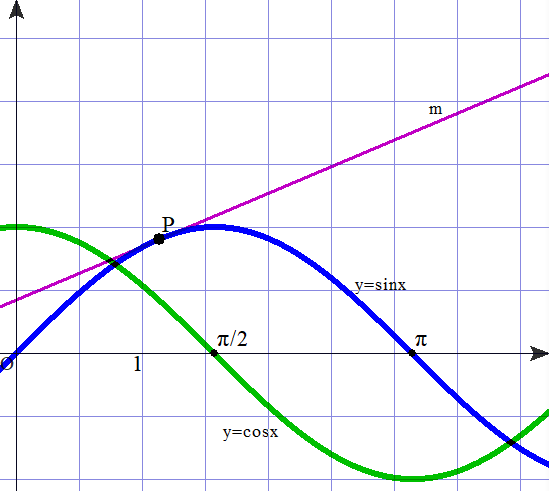
右図で，直線ｍは，y=sin x上の任意の点Ｐにおける接線を表しています．
← ｍは，画面では関数グラフソフト grapes を用いて正確に引かれていますが，実際は，定規を使用して手作業で接線を引きます（アナログ作業）．
さて，この図から ｍ の傾き = f'(x)=cosx となることを図形的に説明してみましょう．いかがですか？
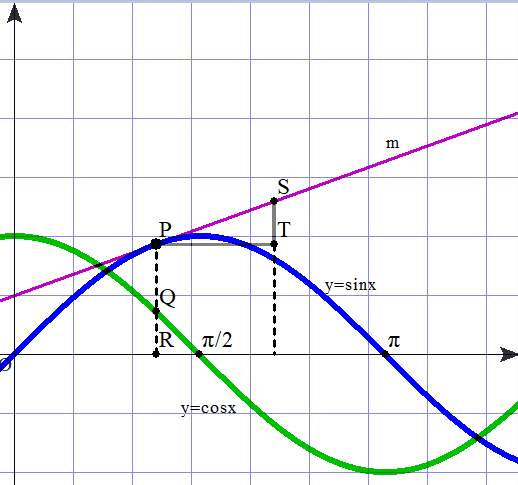
右図で，Ｐは y=sinx 上の任意の点であり，m はＰを接点とする接線です．
また，点Ｑ，Ｒはそれぞれy=cosx上，x軸上にあり，３点Ｐ，Ｑ，Ｒは一直線上に並び，ＰＲ⊥ｘ軸です．
さらに，線分ＰＴ//ｘ軸，ＰＴ＝１，Ｓは ｍ 上の点で，ＳＴ⊥ x軸，とします．
※ この図形的解説はオリジナルです（以前，ある会合でご披露．反応はあまりなかったですね．研修会でなく「会合」がよろしくなかった！）．
＜授業実施上の留意点＞
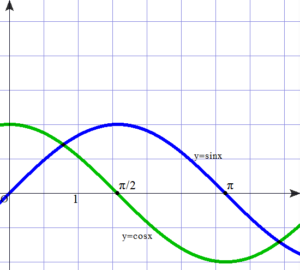
① y=sinx と y=cosx のグラフが同時に描かれたプリントを用意します．その際，点(1,0)は明示します（PT=1 を作図するときに1の長さが必要）．また，ｘ軸とｙ軸の目盛り幅は，１対１ でなければなりません．
② 点Ｐは生徒に任意に打たせますが，45°<x<70° あたりに収まってもらうと実際的になります．
③ 接線mは，アナログ的に，つまり，定規と鉛筆を用いて描くことが必須条件です．接線の公式計算によってｍを求め，正確に描いたプリントを配布してしまったら，本末転倒であってまったく意味をなしません．多少のズレはあったとしても，ほぼST＝QR であることを生徒に「確認」してもらいましょう．
■ 次回のテーマは，「”折る”操作：折り紙は深い！」（仮題）です．
■ 「にほんブログ村」のバナーをClickしていただければ幸いです(最初:左，次:右)．
この話は面白いと思うので、少し考えてみました。
まず、「会合での反応はあまりなかった」のは当然でしょう。研修会でも会合でも、どちらでも反応はイマイチだと思います。図形的解釈をするのは良いが、正弦曲線をコンプー太で描くのが良くない。やっぱアナログですよ。「昭和人類」たるものは「特に」です。
さて、ここで質問。大昔、私達人間が初めて「楕円」を見たのはどんなときでしょうか？
一見、無関係な質問に見えますが、じつは「楕円」と「正弦曲線」とは同じものです。故に、この質問には意味があるのです。
本ブログ2022年6月5日付の
「円錐の斜平面cut ⇒ だ円」を体感する
で、
円柱を斜平面で切り取ったときの切り口がだ円になること
とやっています。木の丸太を斜めに切った切り口が、大昔の人間が初めて見た楕円でしょう。同じ場所に「レストランでよく見かける注文伝票を差し入む器」の写真もあります。
さて、注文伝票を差し入む器の周りに紙を巻き付け、その紙を斜めの切断面に沿って切ります。巻き付けた紙を平面に開くと、あ～ら、不思議。さて、何が現れるでしょうか？
円柱の中身は不要なので、中空の竹を斜めに切った切り口でやりましょう。これ即ち「竹槍」です。
2022年6月5日付記事 “「円錐の斜平面cut ⇒ だ円」を体感する” の、竹槍に入った家具屋姫の絵は最高だ！ 竹槍に入った家具屋姫、万歳！
実際には、巻き付ける紙は少し厚い紙の方が、定規が引っかかるので接線がひきやすい。また、巻き癖がつく紙が良いでしょう。立体であることがよくわかる。
ぷりくら 様
コメントに「面白い」とあり，ありがたいと感じております．
・サインカーブをPCで描くべきかどうかについてです．実際に作業させると、①サインカーブ等のグラフの描き方があまりに粗雑、②接線も同様で，y=x² の場合でも接線がなかなかそれらしい状態に収まらない，という実情があります．目的が「(sinx)’=cosx の体感」でしたので，途上の躓きを避けるため，PCに頼ったところでした．
・楕円と正弦曲線の件は，1/13付けのコメントで内容が理解できました．ありがとうございます．家庭科の教科書で，背広の肩口がほぼ楕円形であり，その際，縫い付ける袖の曲線にサインカーブらしき曲線が登場する話と合致しますね．
・「会合（＝飲み会と数学）」については，まだまだいろいろありまして・・・いつかの機会に話題にします．
まずはお礼まで