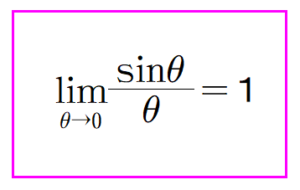θとsinθ の大小(つづき)
前回に引き続き θとsinθ の大小を見極めて,三角関数の微分に関する「あの」重要定理(以下,超定理 ※1)の証明に進みます.

※1 「超定理」↓
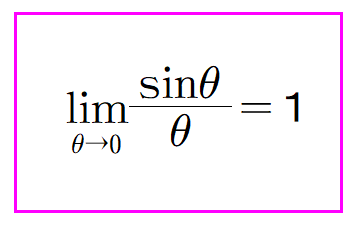
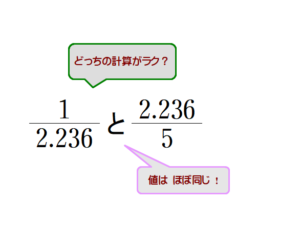
Q1 (突然ですが)上式の計算について意味を解説してください.
A1
1°=π/180≓0.017453(弧度法)
ここで
sin0.017453≓0.017452(関数アプリ:ke!sanより)
よって, θ=0.017453(=1°) とおくと
$$\frac{sinθ}{θ}=\frac{0.017452}{0.017453}=0.999943≓1$$
となることを示している.
■ このように,θ>0 かつ 十分小さいとき,sinθ<θ が成り立ち,さらに,次のことがいえます(θ<0 の場合もOKですが,省略).
$$sinθ≓θ ∴ \frac{sinθ}{θ}≓1 (※2) $$
例の超定理の証明では,※2の左辺で,θ→0 の極限操作をします.
θ≓0 のときは,左辺がほぼほぼ1となるので,θ→0 としたときの極限値は1だろうという推測はできますが,根拠がはっきりしません.
こういうときは,「はさみうちの原理」で極限値を燻り出すこともあり得ます.
そこで,少しばかり脇道にそれます.
発想の転換:面積(体積) ⇒ 辺
■ 図形問題において,通常は,”辺が分かって⇒面積や体積 を求める” です.
しかし,時には,逆の発想もありです.
Q2 右図で,AHの長さを求めてください.ただし,△ABC, △HABは直角三角形とします.
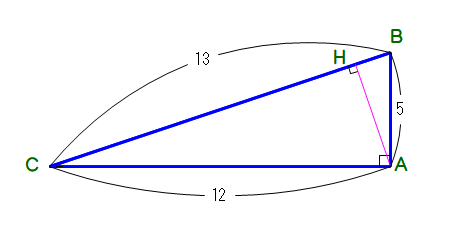
A2 △ABC∽△HBA より相似比を用いる,あるいは,AH=x とおいて,三平方の定理から求める,といった方法が一般的です.
<別解>△ABC=1/2・AC・AB=30
一方,△ABC=1/2・BC・AH
よって,1/2・BC・AH=30 より,AH=60/13
Q3 右図は1辺6の立方体です.三角すいO-PQRについて,頂点Oから底面△PQRへ下ろした垂線の足をHとするとき,OHの長さを求めなさい.
A3 <略解>
① OH=x として三平方の定理を駆使する
② Oを原点とする空間座標内に立方体を置き,平面△PQRと原点Oとの距離公式を用いる
いずれにしてもかなりの腕力が必須です.
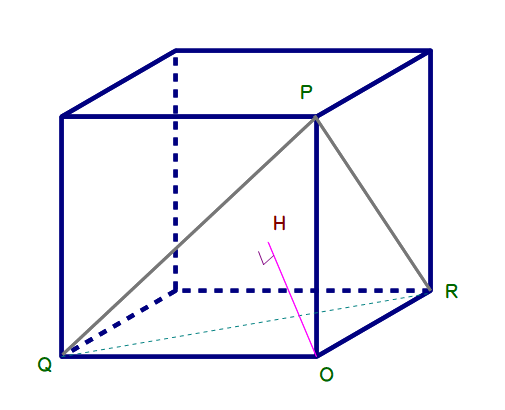

■ A2, A3 の別解は,どんな計算ルートでも面積(体積)値:一定 という結果を逆手にとった,柔らかい発想例ですね.
■ では,本論:超定理の証明に戻りましょう.
はさみうちの原理の”典型”
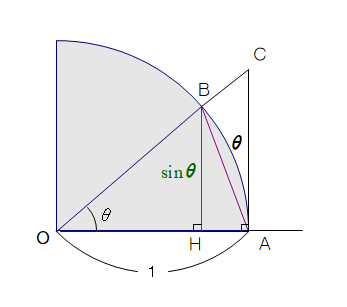
■ 上図で,sinθ<θ は,長さ(距離)比較で何とか解説済みですが,θ<AC で行き詰まっておりました.
■ そこで,長さの直接比較を一旦棚上げにして,面積比較をしてみます.
図で,△OAB<扇形OAB<△OAC が成り立ちます.
ここで,△OAB=1/2・1・sinθ=1/2 sinθ
扇形OAB=1/2・1²・θ=1/2 θ(← 扇形面積公式:1/2r²θ)
△OAC=1/2・1・AC=1/2 tanθ(← AC=tanθ)
よって

■ 1行目は面積比較ですが,2行目が線分と弧長の長さ比較に移っています.
結局,苦労したテーマ「sinθ<θ」も面積比較する中で同時に解決したことになります.
← はじめからそうすれば? いやいや手順を踏むことで理解度が深くなり,応用力もつくものと考えます.
<補足>
■ 次回テーマ「”有理化”への疑問あれこれ」(予定)です.有理化が,単なる式変形・計算練習に映っているかも.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).