全国学テからの「直球」問いかけ
全国学テ(全国学力・学習状況調査)が2007年から計13回実施されてきました(20年は中止).同調査を巡ってはいろいろ議論のあるところですが.教科の中味まで言及した論はあまり見当たりません.算数・数学で問われた内容には.
- やっぱりそうだったのか.多少予想はしていたが・・・正答率の低さに愕然
- 実は,問うこと自体が怖くて避けてきた個所だった.直球勝負された思いだ
- 子供だけでなく指導者にも「メッセージ」が伝わってくる
- 学校では出題しにくいところを突いている
といった声を耳にします(当然,問にもよります).ここでは印象深い例を紹介します.
次は,中数A(2008/4)で出題されたものです.
「証明」の意味&意義がそもそも分かっていない(42%+α)
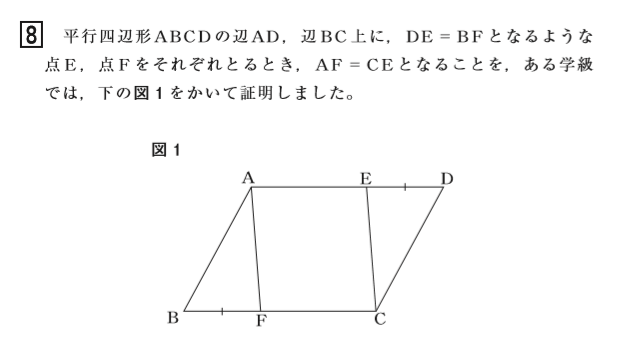
(この後の証明の解説は略します)・・・「2辺挟角」合同条件により△ABF≡△CDE を導く
つまり,この問は「証明しなさい」という内容ではないのです,以下,証明問題のそもそもを問いただす問題文が続きます.
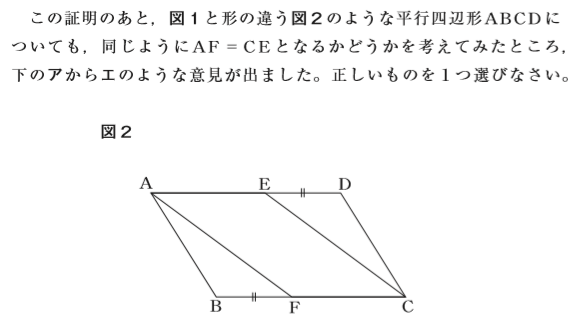

6年前,信州大学准教授小松孝太郎氏は,この問の分析結果から指導改善策を述べております.重なるところもありましょうが,本ブログでも話題にいたします.
(1)正答率(正解:ア):全国58%
4択出題による偶然正解の可能性も併せ考えると,生徒たちの約半数は,実のところ,証明の意義(そもそも論)がよくわかっていないのではないかと言えそうです.
かなりのショックを受けました.自分としては,一例として使用したに過ぎない図形例を用いて導かれた結論に対して「今,板書した図形でのみ通用する性質だ」などと理解している生徒が半数もいるのです.
中学数学到達点の一つである図形証明問題.面白いのですが昔から子供の評判はよろしくない.その克服に向けて合同や相似条件等を列挙して力説するのですが,空回りしそうですね.
(2)全国学テの活用
全国学テに関して「数値比較より結果の活用こそ重要だ」との声に反対する人はいません.しかし,「具体的にどう活用しているの?」が問われています.
本問は,格好の例です.なぜなら,概念理解であり,棒暗記では太刀打ち出来ず,普段の授業姿勢そのものが問われているからです(→ 長期戦略が必要).痛いところを突かれた思いです.
(3)背景
どうしましょう.本設問に対しては,①生徒が,このような問いかけに不慣れ,②読解力不足 を指摘する向きもありましょう.事実,その通りだと思います.
しかし,ここではまず,単純計算とは次元の異なる「証明」に対する教材研究不足,特に生徒の学習心理に関心が薄かったことを,率直に受け止めるべきかと考えます.
(4)対応例
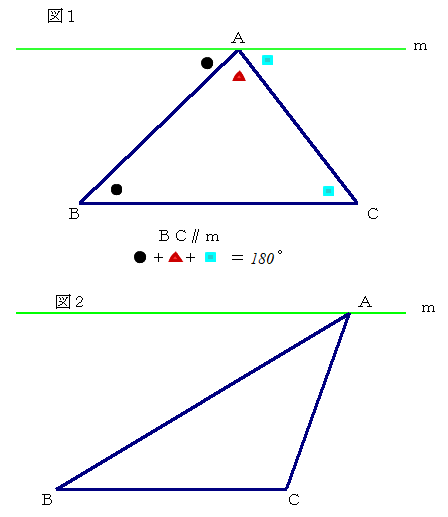
例えば,証明問題の基本の基「三角形の内角の和が180°」を挙げましょう.
図1のように,通常,鋭角三角形を図に示しながら,底辺と平行な直線mを引き,2個所の錯角に着目して,内角和=180° が示されます.
この際,図2の鈍角三角形においては,どうなるのか,やはり,図1と同様にして平行線を引いて論を進めなければならないのか,生徒に話し合いをさせたいところですね.分かる生徒たちがどんな説明をするのか,興味が湧きませんか?
換言すれば,”2つの錯角の活用”という技法に注意・関心・感心を持たせ過ぎた結果,肝心の”すべての三角形で成り立つ”という「証明の意味」確認がぼやけてしまったということです.
くり返しますが,約半数の子どもたちには,証明の意義が伝わっていなかったのです.
(5)テスト出題
対策の一つに「テストに出題する」というやや安直な手があります.しかし,本問のような出題は以下の理由で難しいのです.①教科書や問題集等では同種の問題は見当たらない.したがって,定期テスト等での出題は,おそらく教科内で「却下」される ②全国学テ数学のページ数は,20~30ページ程度.学校での定期テストはB4一枚程度である.本問のようなストーリー性ある大問は物理的に取り上げにくい
授業改善に繋がる出題について,各都道府県の高校入試や私立校の入試,また,全国学テでの取り上げを期待します.
なお,決定過程で「前例がない」ことを理由に却下されることママあります.しかし,新規取り組みは,最初は前例のないところからスタートするのですが・・・.
なお,全国学テについては,いろいろなdataがありますので,再度テーマにしていく予定です.

← 証明の意義(意外性やその着眼点,整頓された形等々,要するに面白さ)が学習者に伝わっていないのではという不安が常にありました.
← ’99東大入試で,①sinθ,cosθの定義,②三角関数の加法定理の証明 が出題され,当時,かなりの話題を呼び,実際,学校,特に予備校での授業展開に影響を与えました.
また,’03同大入試では,「円周率π>3.05」の証明が課され,やはり話題になりました.
■ にほんブログ村のバナーをClickしていただければ幸いです(最初:左.次:右).


