数学用語アレルギー (第2弾)
算数・数学を学ぶ際,新しい単元に入るたびに,新しい「用語」と出会います.そのときの用語なりがかなり”独特“なんですね.結果,抵抗感をもったり,中にはアレルギー反応を起こすヒトもいます.
「商」ってナットクできない
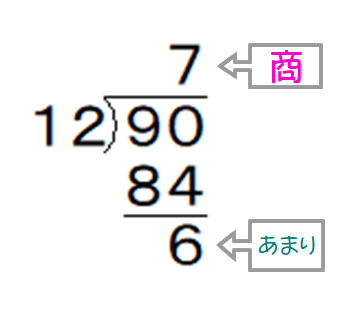
■ 教科書では,小4算数の早い段階で「商」が登場します.割り切れる例を示して「答えを商といいます」と約束(定義)をするのが一般的です.
■ この「商」ですが,子供にとって,当然,唐突感のある言葉ですから何か背景なりを解説したいところ(cf ”あまり”は◎です).
「この割り算の答えですが,特別に商と言うのです」:△
「答えを商と言います」:×
■ 前者が多少ソフトイメージですが,後者は「教科書を教える」素っ気ない解説.どちらも子供の心理・心情に関心がない感じですね.
■ 結論から言えば,中国語表記に沿ったものと考えられます(日本の漢字が中国由来であることを考えると当然なのでしょうが).天から降ってきたような「商」について,何らかのフォローはあるべきですね.
①「商」は,古代中国の王朝(紀元前17c~紀元前11c,殷の俗称)の名前で,その商の国では測量が発達していて割り算も使用されていた.
②殷が周に滅ぼされて,殷人が自らの工芸品を全国に売り歩いたことから,商に「あきない」の意味が生じた(通説)→ 殷王朝人が生計を立てるためお金を稼ぐ行為が「商売」という言葉になった.
このように,測量,商売といった計算文化の発達した古代中国名に関連して,割り算の答に「商」という文字をあてた(らしい).
<参考>blog「みんなで共有,幸せエッセンス(‘13.3.3) ,Yahoo!知恵袋(‘11.4.27)
「式」って何だ?
■ 算数教科書で「しき」という用語は,小1のはじめに現れます.説明抜きで登場することもあり,たいがいは「こたえ」とセットですね.
■ 式とは:①数や文字を演算記号(+,-,×,÷,√ 等)で結びつけたもの ②数学的内容を表現することば(出典「数学小辞典」)とあり,結論に到達するまでの根拠・経緯・過程を示したもの です.
■ 日常用語では,一定のかた,手本,手順 の意味 → 卒業式,式典・・・etc.方程式も拡大解釈すれば含まれそう(手順通りに論を進めるので).
■ 正解のない時代の到来です.算数数学には正解はあるのですが,それは,正解がある問だけを対象にしているからです.これからは「しき・式」をより意識させていくことが重要ですね.
■ かなり効き目あるコトバがあります.それは,「なぜならば」です.この呪文をつねに意識することで,説明全体が論理的な組み立てになっていきます.
「以上」「未満」で迷う(等号は入る?)

■ 「以上・以下・未満」は小4教科書に登場します.けっこう早いですね.「その割にはあいまいな生徒が多いな~」とはある高校教師の愚痴です.
■ 「以上」は「もって(以て)上」であり,その「以て」には「その上に」「そして」の意味があります.
■ 数式では,たとえば,「3以上」は x≧3 と表し,内容は,「x>3 or x=3 」となります.
■ 学習者が中学生以上でしたら,英訳と併用することを強くお薦めします.この時代ですので,キット歓迎されますよ.
xは3以上 ←→ x is greater than or equal to 3
日本人の場合,「3以上」に x=3 が含まれるか否か迷うかも知れませんが,英語圏の子供ならまずそんなことはないはず.なぜなら,その都度[or equal 3]と発音していますから迷いません.
「外分」でうろたえる
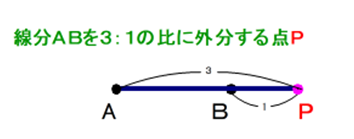
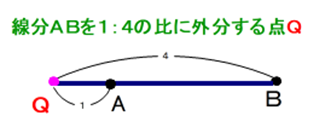
■ 内分はよく浸透していますが,外分はサッパリです.
■ 外分点Pは線分AB上にはありません.なぜなら線分AB上の点は,内分点だからです.
■ 外分比をm:n とします.ペンでなぞりながら外分点Pを打つためのpointは次のとおり.
①A:スタート,B:エンド
②m>nのとき・・・AからBに向かってm進み,その点をPと仮置きして,Pから逆向き(Bに向かって)n進む(戻る).m,n の比案分が適切になるようにPの位置を調整して,改めて外分点Pを決める.
m<nのとき,AからBと逆向きにm進み,その後Bに向き直してn進み,m,nの比案分を考慮しながら外分点Qを決める.
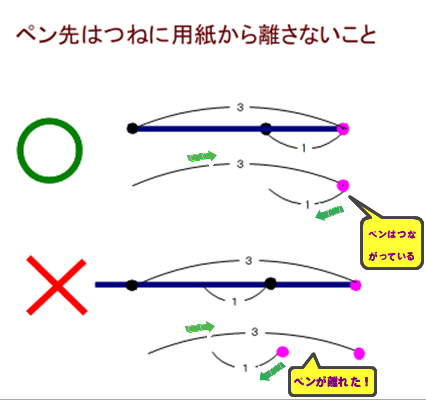
③ペンでなぞる作業中,スタートAからエンドBまでペン先は終始,床(紙面)から離さないこと
<追記>
■ 「数学用語アレルギー」はまだまだたくさんありますので今後も取りあげてまいります.
■ 次回テーマは,「Rさんの『巧みな導入』」です(予定).同じ教材でも導入の在り方で,その後の展開が「天と地」の違いになる場合があります.技法論に陥ることなく,学習者の心理をベースにした印象深い導入例を紹介します.Rさんは当時大学3年生でした.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


