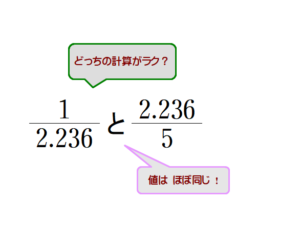
記号「…」って,便利^あいまい
例えば,1/7=0.1428571428…, √2=1.4142135… について,この両者共通に使用されている「…」は雰囲気として分かりますが,何かスッキリしないところありませんか.
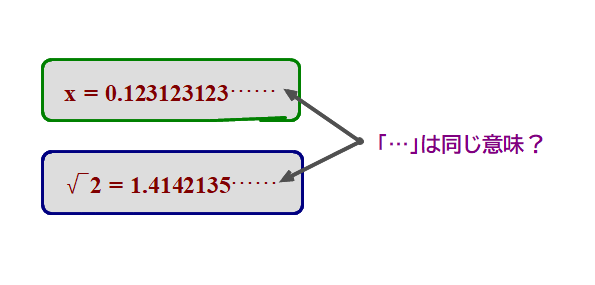
「…」の読み方&意味
■ 読み方は,”3点リーダ“が本家らしいのですが,”テンテンテン”と言っても通じますね.文字変換の際は”さんてん“と入力するとよいでしょう.
数学では,継続や省略 を示す際に用いられます.
なお,一般文では「…」の外にピリオドを用いた「...」が登場するケースが多くありますが,数学では主に前者が使用されています.
教科書デビュー例:2/3の小数表示

■ ある小5算数教科書に 「2÷3=0.66… 割り切れないな」 という解説(コラム)を見つけました.
このように,分数を小数展開する際,割り切れないとき「いくらでも続く」を表す意味で「…」という記号を使っています.日常生活用語の延長で「ワカルでしょ」くらいの扱いでしょうか.
√2 やπ など無理数の小数表示
■ 実数は,有理数と無理数からなります.
①有限小数 or 循環する無限小数 ⇔ 分数表示できる(有理数)
$$\frac{1}{7}=0.142857142857・・・$$
このように長い循環小数となる場合でも,循環ですから「小数点以下n桁目の数は?」という問にも n を用いて式で答えられるわけです(→ 小数点以下100桁目の数は計算で8と答えられる).
ところが
② √2=1.4142135… ,π=3.141592… などの無理数の場合,各桁の出現する数に規則性がありませんから,nを用いての一般的な説明もできません.

■ 循環しない無限小数 は分数表示できない(無理数)ので,小数表示をするよりほかありません.
すると,ある程度の小数点以下からは「…」を用いてイメージで表すことに!
つまり,②の場合は,口惜しい思いで「…」を使用しているのではないか!?と感じます.
■ 以上,「…」が使用される場面についてまとめると
Ⅰ 分数を小数展開したときに,有限桁数の数字の並びが無限にくり返される
2/3=0.666… ,1/7=0.1428571428…
Ⅱ √3などのように,無理数を小数表示すると,各桁の数は規則性なくかつ無限に発生する
√3=1.7320508…
の2タイプがありそうです.
ところがコトは簡単ではありません.Ⅰのパターンはさらなるツッコミが必要です.
0.666…は数なのか?
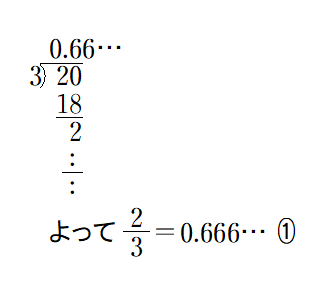
■ このように「分数→小数展開」は算数教科書でも紹介されているくらいですからいいでしょう.
しかし,逆に,0.666…※ が与えられたとき,※が数を表し
0.666……=2/3 である!
と言い切れるかどうかはそんなに簡単なコトではありません.
■ つまり,x=0.666… ② とおいたとき,②が何を示すのか?イメージとしては2/3なのでしょうが,「…」の意味がハッキリしません.
次のような式による解説も見受けます.

一見,論理的なのですが,④-③ の演算が引っ掛かります.
なぜなら,足し算,引き算,かけ算等々の演算は有限値・有限個数の中でルールが作られていますが「…」には無限個の数があります.
■ 無数や無限大の扱いには慎重さが必要です.
例:無限大に5くらい加えても無限大は不変ですね.
すると,∞+5 = ∞ ∴5 = 0 ?!
やはり,ここは新たなルールを作って,0.666…=2/3 を導くべきですね.
⇒ ここに級数という概念を導入する背景があり,「…」にも意味を持たせなければなりません.後日のテーマにします.
<補足>
■ 次回テーマは「通貨のデジタル化」(予定)です.10進法の理解に通貨の果たす役割はきわめて重要です.それが,今,大変なことに!
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).