読解力=国語 ではなく!
■ 題意が「理解できない・できていない」にもかかわらず「解きなさい」と進めるのは一方通行授業の最たるモノです.
■ 「題意が理解できない」要因としては数多くの,また,個別の事情がありましょうが,ここでは2つあげます.

①読解力不足(特に,論理用語に不慣れ)
②題意がイメージできない
■ どちらも克服のハードルは高い(特に,①)ですが,②はやりようによってかなり改善が図れると考えます.
題意のイメージ化
Q1 次の割り算の中で,答えが分子より大きくなるのはどれですか.
① 1÷0.2 ② 3÷3/2 ③ 5÷1.2 ④ 10÷0.001
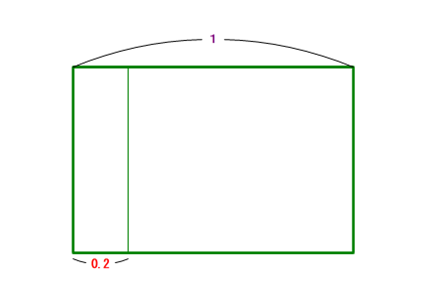

←↑微分の意味は分からなくても,ほとんどの生徒が微分計算はできます.「1÷0.2 の意味はあいまいでも,計算はできる」と本質は同じですね.
■ 正解は当然①,④ですが,実際,各値を計算して解答したら,題意が伝わっていないことになります.
つまり,正解までのプロセスこそ価値ありです.
■ ①の場合,左図のようなイメージをして「要するに,1の中に,0.2がいくつ入っているかを求めればいいのだな.当然,5つ分だ」と認識することです.この姿勢の有無が後々まで響きます.
■ 「計算して答える」と「イメージで答える」を同格・同列に扱うことは間違いです.
■ ①,④ は,後に,tan90°=±∞ の理解と直結します.
■ 実際のところ即,計算し始める子供が多いかも.具体的にどうすれば?
→ 出題の仕方を変えることが解決へのショートカットです.
→ 本問の場合,「・・・分子より大きいのはどれですか.図を書いて説明しなさい」とでもすればよいでしょう.
■ 幸か不幸か,急激な少子化により学年1クラスという学校が増加しています.デメリットは多々ありますが,メリットも探せばあります.
■ 教科担当者が一人 → テスト作成者は一人!自由性を謳歌できます.もちろん責任は伴いますが,自身の作問力向上に繋げましょう.
Q2 すべての実数xについて,
x2-5x+7 > 0 であることを証明しなさい.
■ 平方完成するか,判別式<0 で示される,全くの入門程度問題なのですが,次のような解答と出会うことがママあります.
<誤答例>
x2-5x+7 > 0 ここで,
(x-5/2)2-25/4+7>0
よって, (x-5/2)2+3/4>0
ここで (x-5/2)2≧0 であるから示されたことになる.
■ ときおり見掛ける誤答例です.”計算はしているが,証明はしていない”.単に,証明の形式が分かっていないという判断がされがち.しかし,根はもっと深いところにありそうです.
■ 題意がホントは分かっていないのでしょう.この証明問題の「おもしろさ・不思議さ」(大げさ?)が響いていない段階で,解答に進んでしまっていますね.
■ 本問も次のような出題(またはレポート題)にすれば多少なりとも意義は伝わると考えます.
<レポート題>・・・次回の予習も含めて
式:x2-5x+7 ① について,①が0.75未満となるような実数xを探してください.
※「見つけたヒトにはノートをプレゼントします」などと付け足すのは邪道ですか.
読解力不足は予想以上
例1 男子6名,女子4名 計10名から無作為で3名の委員を選ぶ.その際,女子が少なくとも1名入っている確率を求めなさい.

■ 例1:”少なくとも1名”という条件は”3名とも男子”の余事象を用いると,まともに取り組むより,数段スマートに決着します.
■ ただ,何割かの生徒は,”少なくとも1”の理解がナットクできないでいます.この程度の論理でつまづくと先行きは真っ暗ですね.
■ 例1は数Aで扱います.したがって,学習者は16歳前後です.彼らの日々を想像するとき,日常用語として”少なくとも”という語句はほとんど使用されておらず,”最低1名”などの語句が代替されているのではと推察します.
つまり,”少なくとも1”は,もしかすれば初めて耳にした表現くらいのスタンスでいたほうがよろしいかと.
■ ”少なくとも1”・・・1名はOK?,2名はOK?,3名はOK?などと段階を踏んで理解力を確実にするべきです.その上で,前述したように,「3名とも男子」の余事象の活用を導きましょう.
■ 国語など他教科に責を求めることは非生産的です.数学を通して,日常用語も含め,論理的表現を身に付けさせるくらいの気概で行きましょう.
→ 数学の授業で,「少なくとも」の語義を確認しよう!

■ 近年,興味深い本が出版されました.
「AI vs. 教科書が読めない子どもたち」
です.新井紀子著(東洋経済新報社)
■ 「日本の中高生の多くは,中学校教科書の文書を正確に理解できない」という”驚愕”の実態を次々と紹介しております.そして,学生の寒い実態も.
■ 一部紹介します.
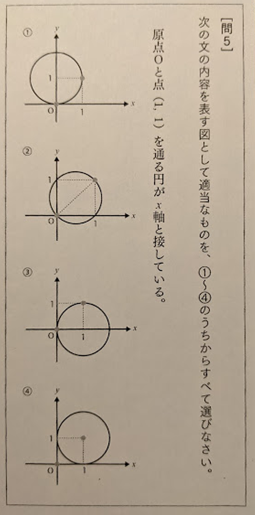
■ 正答率ですが(正解①),中学生19%,高校生32% です.4択の問で,いわゆる偶然正解も含めての結果ですから,実際はさらに深刻になります.
■ 私ども数学教育関係者は,授業にしてもテスト実施にしても,「もしかすれば,題意や説明語句が伝わっていないかも知れない」という思いと怖れをもってコトにあたっていきましょう.
ただし,くどい説明は逆効果になります.
<補足>
■ 次回テーマは「メッセージを感ずるテスト」(仮題)です.テストは学習者が「集中」する絶好の機会です.このチャンスを活かしましょう.
■ 本ブログの冒頭(エンドにも)に,「にほんブログ村」のバナーが2つずつありますが,それぞれClickしていただければ幸いです.