「比例式 ⇒ y=ax」は”ダメ”と言いたい
■ 「yがxに比例する」とは,y=ax (a:比例定数) と書き表せるときですから,y=ax+q ならば一般的に「yはxに比例しない」となります.が,マッテください.

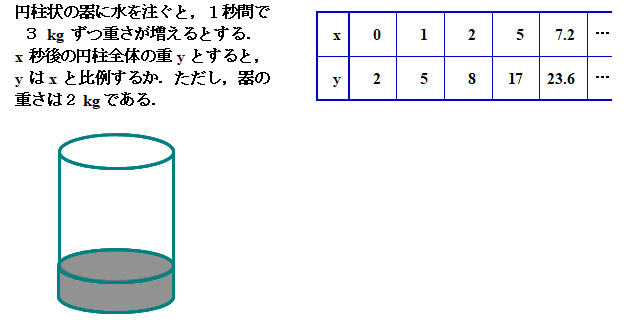
■ 上の表で,y/x (x:0以外)を計算すると,5/1, 8/2, 17/5・・・となり一定値となりませんから,確かにyとxは比例関係にはありません.しかし,ここで思考停止させてしまったら,学習者が不幸です.
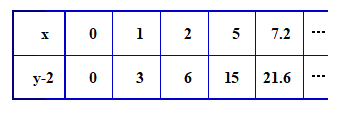
■ 次の表ではどうでしょう.(y-2)/x の値は,常に3 で一定しています.
■ つまり,y-2 は x と比例しているのです.
■ 一般化しますと, y=ax+q ⇒ y-q=ax と変形し,y-q を一文字(Y)と見なすと,Y は x と比例する と言えます.
文字を「固定」しない

■ この y-q を一文字と見なすことに慣れていない,見なせない生徒が少なからずいます.
■ 一つの理由は,彼らの多くは,y-q を y,-,q とパーツごとに分解して見つめてしまう,つまり,「文字と目が近すぎる」のです(数学近視眼!).
■ グラフで考えてみましょう.
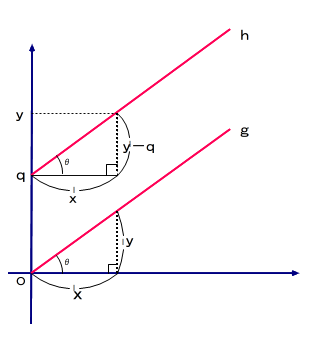

■ 点(x,y)の無数の集まりは,直線gを形成しますが,この説明をキチンと理解すると後々に役に立ちます(発展性あり).
■ さて,上のグラフは直線gをy軸方向にqだけ平行移動した様子を表しています.

”比例”のエッセンスとは?
■ 比例の本質&原点は,「相似比一定(tanθ)にあり,グラフに示すと点(2変数)が直線状に並ぶ」ことです.そのグラフを平行移動する・しないということは,本質から外れます.
■ したがって,y=3x+2 において,「yはxと比例しないのだ!」と力説する向きには賛同しかねます.
文字式は,グラフで体感して身に付けよう
■ 複雑な文字式や関数式も,グラフで確認出来る場合は,画像的に体感しながら理解を深めていきましょう.
■ 下図で,△BACと△PAQ に注目してください.
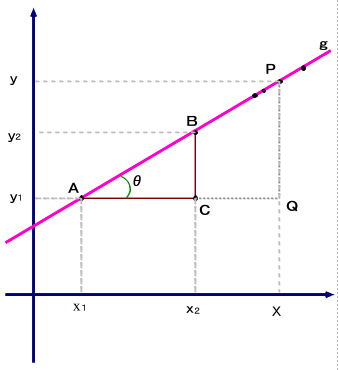

■ ④を公式として覚えるとき,まず直線のグラフを書き,二つの相似な直角三角形を見出す.そしてtanθをおそれぞれ辺の比から書き出す.この手順をくり返すと,自然に④が思い浮かび,かつ,身に付くようになります.
<補足>
■ 次回テーマは「題意をしっかりつかむ」(仮題)です.題意があいまいなママ「解け」と言われると辛いですよね.
■ 本ブログの冒頭(エンドにも)に,「にほんブログ村」のバナーが2つずつありますが,それぞれClickしていただければ幸いです.


