πと誕生日
■ 円周率π は何とも不思議かつ魅力ある数ですね.本稿では実数の確認,πの無限小数表示にまつわる「摩訶不思議さ」を紹介します.また,πと聞くと 円周率≓3.14 だけで思考停止する,数学的にはよろしくない例を確認しましょう.
π は 循環しない無限小数
■ 実数とはどんな数を言うのか,改めて確認しましょう.
{・・・-5, -3, -1/2 ,0 ,1/3 ,1 ,√2 , π ,4.3 ,・・・}など,すべて実数です.粗い言い方をすれば,数直線x軸上の点が実数に対応します.
時間をたどると,小学~中学まで習う数が実数です(高校で虚数と出会います).

■ 0.123=123/1000 のように,有限小数は分数表記できます.つまり有理数です.
また,0.123123123・・・=123/999 のように循環小数も有理数です(証明は高校数学レベルでさほど難しくない).
■ ところが,πは無理数です(証明はかなり大変).
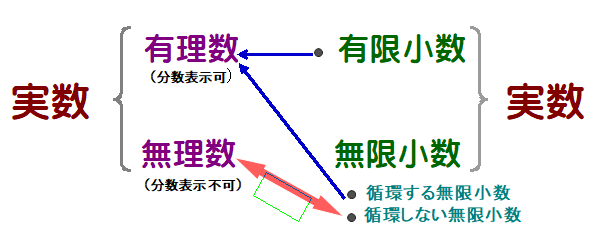
■ 上図を見てください.実数をすべて小数で表すことにすると,無理数であるπは,循環しない無限小数ということになります.
■ この論理の要は,実数は,①有限小数,②循環無限小数,②’非循環無限小数 の3パターンに分けられ,かつ,これ以外にはなく,①②でなければ,②’しかない という認識をトコトン持てるかどうかです.この認識が甘いと,√2 や π の永遠に続く小数展開を見てもカンドー出来ませんね.また,同様の発想で進める,背理法による証明一般も理解に苦しむことでしょう.
■ 計算力向上=論理的思考力向上 と勘違いしている向きもあります.論理的説明能力アップの対策にはどんなものがあるでしょうか?
対応策を一つ提案します.それは,論理展開に関する問いかけを評価と直結させる,つまり,試験に出題する ことです.あるいは,ペーパーテストに拘泥せず口頭試問の導入はいかがですか.テスト=「一斉・50分」の形に柔軟性を持たせるべきかと.出来ない理由はヤマとありましょうが,一部適用でも構いません.出来る可能性の尊重を!.
かつて東大入試(’99)では三角関数の加法定理の証明が課せられました.「してやられた!」という声も結構ありました.
ただひたすら円周率100万桁・・・
■ 数年前,ジュンク堂で何とも言えない本と出会いました.手招きされるようについ購入してしまった本の紹介です.

■ まず,題名が「π・・・円周率100万桁表・・・」,出版社名が「暗黒通信団」ときた!.中味は以下のようです.


■ 各ページごと,1万桁ずつ,つまり,全体で100ページにわたり,円周率を計100万桁までひたすら印刷したものです.もちろん,3からスタートし,100万桁目は1でした.
■ 失礼ながらこの本に需要はあるのでしょうか?
発刊が約四半世紀前で今日でも販売されていることから,ヒトを惹きつける何かがありますね.
■ 巻末ページ:筆者と読者とのやりとりが面白いです.
Q「何を血迷ってこんな本を作ったのですか?」 A「そんなふうに思う人はこの本を買わないと思います」
Q「著作権はどうなっていますか?」 A「円周率は創造物ではなく,(略)著作権を放棄します.(略)」

■ 価格はどうなっているでしょう!! やられました! 当ててみてください.
■ この冊子が,中高(小・大でも)の各クラスに何気なくぶら下がっている光景,見てみたい!ですね.
円周率の中に ”誕生月日” を発見
■ くり返しますが,πは無理数ですので,小数展開すると巡回しない無限小数となります.各桁で登場する数に規則性はありません.
ということは,何桁かの任意の数を指定すれば,無限に並ぶ数列の中の”どこかに存在する”のではなかろうか,と考えられます.
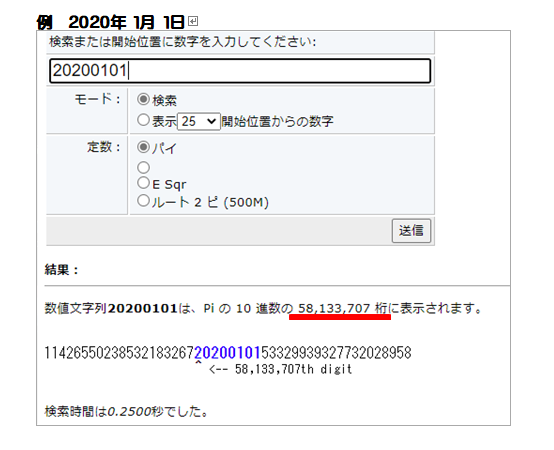
■ 本稿は,2020年11月20日前後に作成しています.結論を急ぎますが,上6桁「202011」までなら先程の「π」冊子の中に発見出来ました.632,803桁目から202011が並んでいます.

■ およそ6桁までの数ですと,「π」冊子(100万桁)内で見つけられそうですが,7桁以上になるとかなり困難です.
■ 7桁以上の数は,次のサイトで調べてください.ご自身の誕生月日を探しましょう.
例:1999年5月9日 → 19990509
きっと小数点以下1億桁前後までで見つかりますよ.
Irrational Numbers Search Engine (subidiom.com)
■ なお,日本数学検定協会では同じテーマを深堀しています.そちらも訪問しましょう.
「弧度」の棒暗記
■ 「π:円周率」の狭い捉え方で縛られ,かつ,弧度法を習うと「π=180°」という単位換算値を棒暗記している高校生たちが大勢います.
さらに,角と言えば,30°,45° とそれらの倍数角(有名角)に絞ってしまい,中には,三角関数値表を丸暗記させる向きもあります.数学が年号暗記と同列になってしまったのかとヂグヂたる思いです.百歩譲り「点数を取らせなきゃ」は分かったとしても,「三角比の基礎だから」は×です.この場合,基礎の定義が間違っていると断言します.
したがって棒暗記させられたヒトは
「sin1, sin2, sin3, sin4 を大小順に並べよ」(類題:法政大学)などと問われると面食らってしまうし,蔵王スキー場の傾斜角38°のスロープは極めてキツく,上に立つと垂直に落ちるような感覚になるというような話にもあまり興味を持たないのです.
π=3.14…と唱えられても,棒暗記のサンテンイチヨン…ですのでお経のようなもの.だから,sin3≓sinπ=0 と論理が流れないのでしょう.弧度法については,後日のテーマにする予定です.
<追記>
■ 次回テーマは,「y=ax+b :yはxと比例しない は正しいのか?」です(予定).正しいのですが「狭い了見」と言わざるを得ませんね.
■ 「にほんブログ村」のバナーをclickしていだだければ幸いです(はじめに左, 次に右).